Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Для точного выражения массы следует найти предел суммы (*) при условии и каждая частичная область стягивается к точке. Тогда

б) Статические моменты и центр тяжести пластинки.

Перейдём теперь к вычислению статических моментов рассматриваемой пластинки относительно осей координат. Для этого сосредоточим в точках массы соответствующих частичных областей и найдем статические моменты полученной системы материальных точек :

Переходя к пределу при обычных условиях и заменяя интегральные суммы интегралами, получим

Находим координаты центра тяжести :

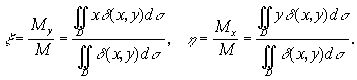
Если пластинка однородна, т.е. то формулы упрощаются :

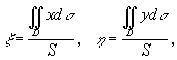где S - площадь пластинки.

 

в) Моменты инерции пластинки.

Моментом инерции материальной точки Р с массой m относительно какой-либо оси называется произведение массы на квадрат расстояния точки Р от этой оси.

Метод составления выражений для моментов инерции пластинки относительно осей координат совершенно такой же, какой мы применяли для вычисления статических моментов. Приведем поэтому только окончательные результаты, считая, что :

Отметим еще, что интеграл называется центробежным моментом инерции; он обозначается .

В механике часто рассматривают полярный момент инерции точки, равный произведению массы точки на квадрат ее расстояния до данной точки - полюса. Полярный момент инерции пластинки относительно начала координат будет равен

 

4. Вычисление площадей и объёмов с помощью двойных интегралов.

а) Объём.

Как мы знаем, объем V тела, ограниченного поверхностью , где - неотрицательная функция, плоскостью и цилиндрической поверхностью, направляющей для которой служит граница области D, а образующие параллельны оси Oz, равен двойному интегралу от функции по области D :

Рекомендуем скачать другие рефераты по теме: доклад по химии, банк рефератов и курсовых.



Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки