Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Примеры. 1) Найдём двойной интеграл от функции

по прямоугольной области D

Геометрически I выражает объём четырёхугольной призмы

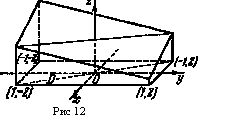
(рис.12), основанием которой служит прямоугольник D, усечённый плоскостью .

Возьмём повторный интеграл сначала по y, затем по x:

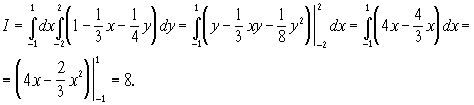
То же самое получим, интегрируя сначала по x, а затем по y:

 

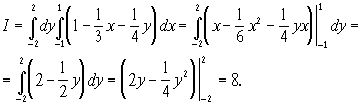
2) Вычислим двойной интеграл

по области D, ограниченной линиями y=x и y=x2. Область D

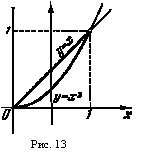
изображена на рис.13. Интегрируя сначала по y, а потом по x,

получаем

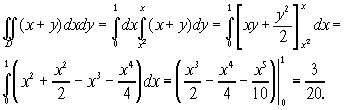
Правильность результата можно проверить, изменив порядок интегрирования :

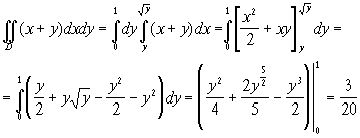
Вычислим объём тела, ограниченного цилиндрическими поверхностями и плоскостью z=0 (рис.14,а).

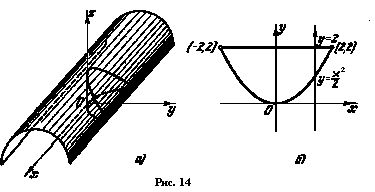
Поверхность, ограничивающая тело сверху, имеет уравнение z=4-y2. Область интегрирования D получается в результате пересечения параболы с линией пересечения цилиндра z=4-y2 и плоскости z=0, т.е. с прямой y=2 (Рис. 14, б). Ввиду симметрии тела относительно плоскости Oyz вычисляем половину искомого объёма :

Рекомендуем скачать другие рефераты по теме: доклад по химии, банк рефератов и курсовых.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки