Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Предел этой суммы, когда наибольший из диаметров площадок - стремится к нулю, мы будем называть площадью поверхности, т. е. по определению положим

(2)

Займемся теперь вычислением площади поверхности. Обозначим через угол между касательной плоскостью и плоскостью Оху.

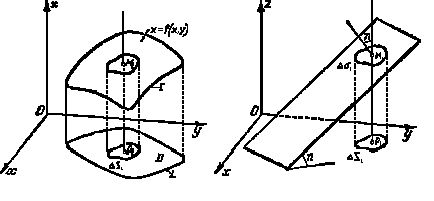
Рис.20 Рис.21

На основании известной формулы аналитической геометрии можно написать (рис.21)

или

(3)

Угол есть в то же время угол между осью Oz и перпендикуляром к плоскости (1). Поэтому на основании уравнения (1) и формулы аналитической геометрии имеем

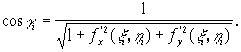Следовательно,

Подставляя это выражение в формулу (2), получим

Так как предел интегральной суммы, стоящей в правой части последнего равенства, по определению представляет собой двойной интеграл 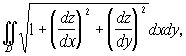то окончательно получаем

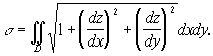(4)

Это и есть формула, по которой вычисляется площадь поверхности

Если уравнение поверхности дано в виде или в виде то соответствующие формулы для вычисления поверхности имеют вид

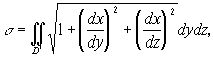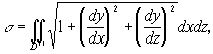(3’)

(3’’)

где D’ и D’’ - области на плоскостях Oyz и Oxz, в которые проектируется данная поверхность.

а) Примеры.

Пример 1. Вычислить поверхность сферы

Решение. Вычислим поверхность верхней половины сферы (рис.22). В этом случае

Рекомендуем скачать другие рефераты по теме: доклад по химии, банк рефератов и курсовых.



Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки