Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Ответ: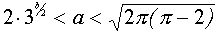

II. Неравенства с параметрами. § 1. Основные определения

Неравенство

¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x), (1)

где a, b, c, …, k – параметры, а x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.

Любая система значений параметров а = а0, b = b0, c = c0, …, k = k0, при некоторой функции

¦ (a, b, c, …, k , x) и

j (a, b, c, …, k , x

имеют смысл в области действительных чисел, называется системой допустимых значений параметров.

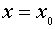называется допустимым значением х, если

¦ (a, b, c, …, k , x) и

j (a, b, c, …, k , x

принимают действительные значения при любой допустимой системе значений параметров.

Множество всех допустимых значений х называется областью определения неравенства (1).

Действительное число х0 называется частным решением неравенства (1), если неравенство

¦ (a, b, c, …, k , x0)>j (a, b, c, …, k , x0)

верно при любой системе допустимых значений параметров.

Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.

Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.

Два неравенства

¦ (a, b, c, …, k , x)>j (a, b, c, …, k , x) и (1)

z (a, b, c, …, k , x)>y (a, b, c, …, k , x) (2)

называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.

§ 2. Алгоритм решения. Находим область определения данного неравенства. Сводим неравенство к уравнению. Выражаем а как функцию от х. В системе координат хОа строим графики функций а =¦ (х) для тех значений х, которые входят в область определения данного неравенства. Находим множества точек, удовлетворяющих данному неравенству. Исследуем влияние параметра на результат. найдём абсциссы точек пересечения графиков. зададим прямую а=соnst и будем сдвигать её от -¥ до+¥ Записываем ответ.

Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy.

§ 3. Примеры

I. Для всех допустимых значений параметра а решить неравенство

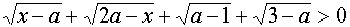
Рекомендуем скачать другие рефераты по теме: реферат на тему человек, диплом на заказ.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки