
Графическое решение уравнений, неравенств, систем с параметром
Категория реферата: Рефераты по математике
Теги реферата: контрольная работа 8, шпори на пятках
Добавил(а) на сайт: Хребтов.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата
Решение.
В области определения параметра а, определённого системой неравенств
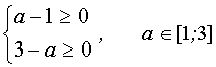
данное неравенство равносильно системе неравенств
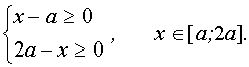
Если 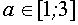 , то решения исходного неравенства заполняют отрезок
, то решения исходного неравенства заполняют отрезок 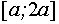 .
.
Ответ: 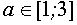 ,
, 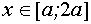 .
.
II. При каких значениях параметра а имеет решение система
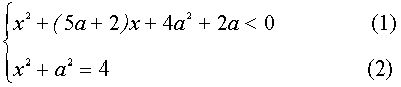
Решение.
Найдем корни трехчлена левой части неравенства –
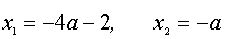 (*)
(*)
Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен
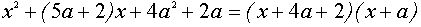
сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован
ной области с окружностью, где 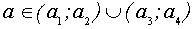 , а значения
, а значения 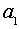 и
и 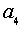 находятся из системы
находятся из системы
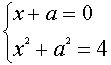
а значения 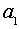 и
и 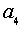 находятся из системы
находятся из системы
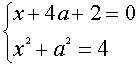
Решая эти системы, получаем, что
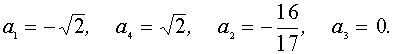
Ответ: 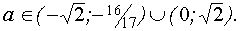
III. Решить неравенство 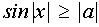 на
на 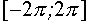 в зависимости от значений параметра а.
в зависимости от значений параметра а.
Решение.
Находим область допустимых значений –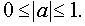 Построим график функции в системе координат хОу.
при
Построим график функции в системе координат хОу.
при 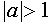 неравенство решений не имеет.
при
неравенство решений не имеет.
при 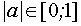 для
для 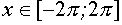 решение х удовлетворяет соотношению
решение х удовлетворяет соотношению 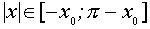 , где
, где 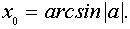
Ответ: Решения неравенства существуют при 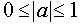
Рекомендуем скачать другие рефераты по теме: реферат на тему человек, диплом на заказ.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 | Следующая страница реферата