Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

           (5)

Причем | Z | < R,  R ®  ¥ .>

Формулы ЭЙЛЕРА.

Применим разложение (3) положив, что Z = ix  и   Z= - ix;

                                                        (6)

Аналогично взяв Z = - ix  получим :

                                                      (7)

Из (6) и (7) можно выразить т.н. формулы Эйлера :

                 (8)

В общем случае :

    (9)

Известно, что :

      (10)

Тогда из (9) и (10) вытекает связь между тригонометрическими и гиперболическими косинусами и синусами:

Ряд ЛОРАНА.

Пусть функция f(z) является аналитической функцией в некотором круге радиусом R, тогда ее можно разложить в ряд Тейлора (2). Получим тот же ряд другим путем.

ТЕОРЕМА 1.

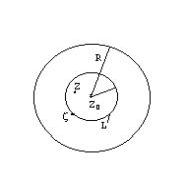
Однозначная функция  f(Z) аналитическая в круге радиусом  |Z-Z0| < R раскладывается в сходящийся к ней степенной ряд по степеням Z-Z>0.

Опишем в круге радиусом R окружность r, принадлежащую кругу с радиусом R.

Возьмем в круге радиуса r точку Z, а на границе области точку z , тогда  f(z) будет аналитична внутри круга с радиусом r и на его границе. Выполняется условие для существования интеграла Коши :

                                                                                        (13)

Рекомендуем скачать другие рефераты по теме: семья реферат, диплом купить.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки