Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

  и

Свойства линейности изображения.

Теорема : изображение суммы нескольких функций умноженное на постоянные равны сумме изображений этих функций умноженных на те же постоянные.

Если , то , где

Теорема смещения : если функция F(p) это изображение f(t), то F(a+p) является изображением функции e-at f(t)                                 (4)

Доказательство :

Применим оператор Лапласа к левой части равенства (4)

Что и требовалось доказать.

Таблица основных изображений:

F(p)	f(t)	F(p)	f(p)

Изображение производных.

Теорема. Если , то справедливо выражение :

                                             (1)

Доказательство :

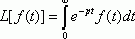
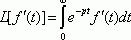
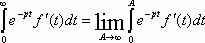                           (2)

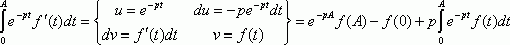    (3)

Подставляя (3) в (2) и учитывая третье условие существования функции Лапласа имеем :

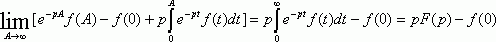
Что и требовалось доказать.

Пример: Решить дифференциальное уравнение :

  Если x(0)=0   и x’(0)=0

Предположим, что x(t) – решение в области оригиналов и , где - решение в области изображений.

Рекомендуем скачать другие рефераты по теме: семья реферат, диплом купить.



Предыдущая страница реферата | 3  4  5  6  7  8  9  10  11  12  13 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки