Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

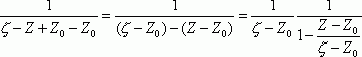                (11)

Поскольку

, то выражение 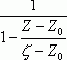 можно представить как сумму бесконечно убывающей геометрической прогрессии со знаменателем , т.е. :

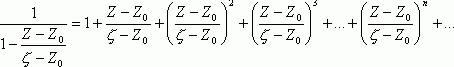
                     (12)

Представим равномерно сходящимся рядом в круге радиуса r, умножая (12) на 1/(2pi) и интегрируя по L при фиксированном  Z, получим : слева интеграл (13) который равен f (Z), а справа будет сумма интегралов :

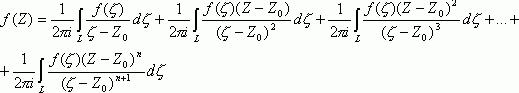
Обозначая , получим :             (14)

Это разложение функции f (Z) в круге R в ряд Тейлора. Сравнивая (14) с рядом (2) находим, что                                                                                  (15)

ТЕОРЕМА 2.

Если однозначная функция f(Z) аналитична вне круга с радиусом r с центром в точке Z0 для всех Z выполняется неравенство r < |Z-Z>0 |, то она представляется рядом :

                                                                        (16)

где  h - ориентированная против часовой стрелки окружность радиуса r (сколь угодно большое число). Если обозначить   (17) , получим :

                                                (18)

ТЕОРЕМА 3.

Если однозначная функция f(Z) аналитическая в кольце Z< |Z-Z>0 |0 существует M>0 и S0³0 такие, что выполняется условие : |f(t)|S0t

Рассмотрим функцию f(t)×e-pt , где р – комплексное число р = ( а + i b).

                                  (1)

Применим к этому соотношению формулу Эйлера :

Проинтегрировав это равенство получим :

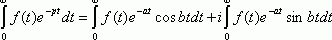                (2)

Оценим левую часть равенства (2) :

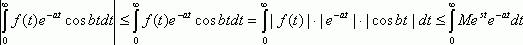
А согласно свойству (3)  |f(t)| < Me >S0t

Рекомендуем скачать другие рефераты по теме: семья реферат, диплом купить.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки