Рефераты | Рефераты по математике | История статистики История статистики Категория реферата: Рефераты по математике Теги реферата: рассказы, промышленность реферат Добавил(а) на сайт: Felicata. Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата	36	116,4	18,7
Итого:	223,8	0	182	16,1	223,5

1. По методу укрупнения интервалов имеем новые укрупненные поквартально уровни ряда динамики:

у1 = 18,6 + 17,3 + 18,9 = 54,8;

y2 = 18,2 + 17,9 + 19,1 = 55,2 и т.д.

Выровненный ряд динамики примет вид:   54,8    55,2    56,3    57,5.

То есть наблюдается четно выраженная тенденция увеличения выпуска молдингов цехом за 1989 г.

2. Употребляя те же данные, применим метод скользящей средней, используя семичленную скользящую среднюю. Тогда:

 =  = 18,5;

 =  = 18,4 и т.д.

Выравненный с помощью семичленной скользящей средней ряд динамики примет вид:   18,5    18,4    18,6    18,7    18,8    19,0.

Таким образом, подтверждается тенденция увеличения выпуска молдингов в течение 1989 г.

3. Используя метод отсчета от условного нуля введем условное обозначение времени "t", придав ему определенные значения так, чтобы ∑t = 0 (см. табл. 6.2).

Судя по выявленной с помощью двух предыдущих методов тенденции выпуска молдингов в течение года, можно сказать, что наиболее вероятна линейная зависимость данного распределения от времени "t" и данному распределению соответствует уравнение прямой  = a0 + a1t.

Для нахождения параметров a0 и a1 используем систему уравнений

 ,

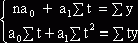так как ∑t = 0, о имеем

a0 =  =  = 18,6;

a1 =  =  = 0,09.

Следовательно, уравнение прямой примет вид:

 = 18,6 + 0,09t и будет в данном случае искомым, так как ∑y = ∑.

Тема 7. Показатели вариации

Наряду со средней величиной, характеризующей типичный уровень варьирующего признака, около которого колеблются отдельные значения признака, рассматривают показатели вариации (колеблемости) признака, позволяющие количественно измерить величину этой колеблемости.

К показателям вариации относят: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Простейшим показателем вариации является размах вариации, который рассчитывается по следующей формуле:

R = Xmax – Xmin,

где Xmax, Xmin - соответственно, максимальное и минимальное значения признака в исследуемой совокупности.

Размах вариации характеризует диапазон колебаний признака в изучаемой совокупности и измеряется в тех же единицах, в которых выражен признак.

Рассчитывают среднее линейное отклонение, которое бывает невзвешенное и взвешенное. Если каждое значение признака встречается в совокупности один раз, то применяется формула среднего линейного отклонения невзвешенного:

,

где x - значение признака;

n - количество вариант.

Если имеется некоторая повторяемость значений признака, то применяется формула среднего линейного отклонения взвешенного:

,

где m - частота.

Среднее линейное отклонение характеризует абсолютный размер колеблемости признака около средней и измеряется в тех же единицах, в которых выражен признак.

Наиболее точным показателем вариации является среднее квадратическое отклонение. Для его определения предварительно рассчитывают показатель дисперсии. Дисперсия невзвешенная определяется по формуле:

σ2 =.

Дисперсия взвешенная определяется по формуле:

σ2 =.

Тогда, соответственно, для расчета среднего квадратического отклонения невзвешенного используют формулу:

σ =,

а для расчета среднего квадратического отклонения взвешенного - следующую формулу:

σ =.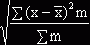

Рекомендуем скачать другие рефераты по теме: сеть рефератов, бесплатные рассказы.



Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки