Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата

 

 

а площадь под кривой на заданном интервале X определяет вероятность попадания в этот интервал.

Чаще всего закон нормального распределения используется для нормированной случайной величины

Z = (X – m ) /s , {2–11} у которой M(Z)=0; D(Z)=1. {2–12}

Отметим ряд других особенностей этого распределения, полагая его нормированным.

· Доказано, что целый ряд “классических” распределений (как дискретных, так и непрерывных) стремятся к нормальному при непрерывном изменении их внутренних параметров.

· Симметрия нормального распределения позволяет достаточно просто оценивать вероятность “попадания” случайной нормированной величины в заданный диапазон. Очень часто в прикладной статистике приходится использовать понятие “маловероятного” значения. Для нормированной величины с нормальным распределением вероятность попадания в диапазон ± 3s составляет 0.9973 (правило “трех сигм”).

· Особую роль играет нормальное распределение при решении вопросов о “представительности” наблюдений. Оказывается, что работа с выборочными распределениями в большинстве случаев позволяет решить проблему оценки наших предварительных выводов, предположений, гипотез – с использованием разработанных и теоретически обоснованных приемов на базе нормального закона.

Распределения выборочных значений параметров нормального распределения

Пусть у нас имеется некоторая непрерывная случайная величина X , распределенная нормально с математическим ожиданием m и среднеквадратичным отклонением s . Если мы имеем n наблюдений над такой величиной (имеем выборку объемом n из генеральной совокупности) , то выборочные значения Mx и Sx являются также случайными величинами и нам крайне важно знать их законы распределения. Это необходимо как для оценки доверия к этим показателям, так и для проверки принадлежности исходного распределения к нормальному. Существует ряд теоретически обоснованных выводов по этой проблеме:

· величина 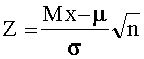имеет нормированное нормальное распределение, что позволяет оценивать Mx при заранее известной дисперсии;

· величина 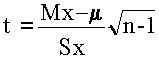имеет так называемое распределение Стьюдента, для которого также имеется выражение плотности вероятности и построены таблицы;

· величина 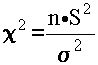имеет распределение "хи–квадрат", также с аналитической функцией плотности и рассчитанными по ней таблицами.

Отметим, что распределения Стьюдента и "хи–квадрат" имеют свой внутренний параметр, который принято называть числом степеней свободы. Этот параметр полностью определяется объемом выборки (численностью наблюдений) и выбирается обычно равным m =(n – 1).

Взаимосвязи случайных величин Парная корреляция

Прямое толкование термина "корреляция" — стохастическая, вероятная, возможная связь между двумя (парная) или несколькими (множественная) случайными величинами.

Рекомендуем скачать другие рефераты по теме: скачать доклад бесплатно, вирусы реферат.



Предыдущая страница реферата | 8  9  10  11  12  13  14  15  16  17  18 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки