Рефераты | Рефераты по математике | Математические модели в естествознании | страница реферата 9 | Большая Энциклопедия Рефератов от А до Я
Большая Энциклопедия Рефератов от А до Я
  • Рефераты, курсовые, шпаргалки, сочинения, изложения
  • Дипломы, диссертации, решебники, рассказы, тезисы
  • Конспекты, отчеты, доклады, контрольные работы


    • Рефераты | Рефераты по математике | Математические модели в естествознании


    Рефераты | Рефераты по математике | Математические модели в естествознании

    Математические модели в естествознании




    Категория реферата: Рефераты по математике
    Теги реферата: договор реферат, инновационная деятельность
    Добавил(а) на сайт: Добромила.



    Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 |



    Рефераты | Рефераты по математике | Математические модели в естествознании.

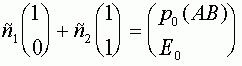    Получаем 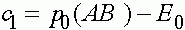Рефераты | Рефераты по математике | Математические модели в естествознании и Рефераты | Рефераты по математике | Математические модели в естествознании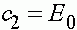. В результате получаем решение системы (6):

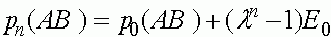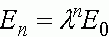    Рефераты | Рефераты по математике | Математические модели в естествознании,

    Рефераты | Рефераты по математике | Математические модели в естествознании .

    Совершенно аналогично исследуется изменение частот гамет (ab), (Ab), (aB):

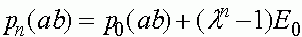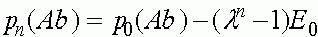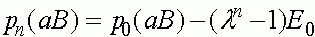    Рефераты | Рефераты по математике | Математические модели в естествознании ,

    Рефераты | Рефераты по математике | Математические модели в естествознании ,

    Рефераты | Рефераты по математике | Математические модели в естествознании .

    Из полученных формул следует, что при Рефераты | Рефераты по математике | Математические модели в естествознании (с ростом номера поколения) Рефераты | Рефераты по математике | Математические модели в естествознании и

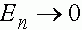    Рефераты | Рефераты по математике | Математические модели в естествознании ,Рефераты | Рефераты по математике | Математические модели в естествознании , Рефераты | Рефераты по математике | Математические модели в естествознании , Рефераты | Рефераты по математике | Математические модели в естествознании.

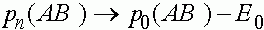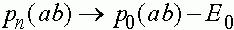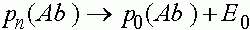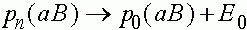    Тем самым, частоты гамет стремятся к состоянию равновесия, которое не достижимо за конечное число поколений. Частоты генотипов определяются через частоты гамет, а, следовательно, также стабилизируются. В отличии от случая, соответствующего закону Харди -Вайнберга, стабилизация в первом поколении не наступает.

    Как уже говорилось, начальное состояние равновесно, т.е. частоты гамет в дальнейшем не меняются, если 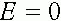Рефераты | Рефераты по математике | Математические модели в естествознании, т.е.

    Рефераты | Рефераты по математике | Математические модели в естествознании.

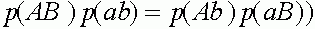    Исследуем условия равновесности. Рассмотрим частоты генов

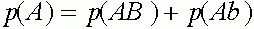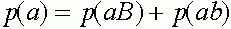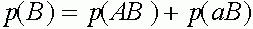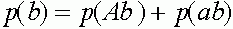    Рефераты | Рефераты по математике | Математические модели в естествознании, Рефераты | Рефераты по математике | Математические модели в естествознании,

    Рефераты | Рефераты по математике | Математические модели в естествознании, Рефераты | Рефераты по математике | Математические модели в естествознании.

    Легко видеть, что 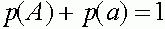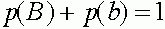Рефераты | Рефераты по математике | Математические модели в естествознании, Рефераты | Рефераты по математике | Математические модели в естествознании. Прямые вычисления показывают:

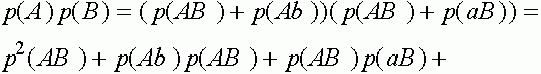
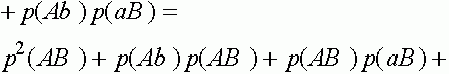
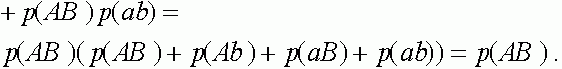
    Рефераты | Рефераты по математике | Математические модели в естествознании

    Рефераты | Рефераты по математике | Математические модели в естествознании

    Рефераты | Рефераты по математике | Математические модели в естествознании

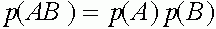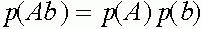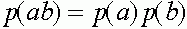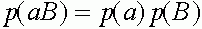    Таким образом, Рефераты | Рефераты по математике | Математические модели в естествознании. Совершенно аналогично: Рефераты | Рефераты по математике | Математические модели в естествознании, Рефераты | Рефераты по математике | Математические модели в естествознании, Рефераты | Рефераты по математике | Математические модели в естествознании.

    В равновесных состояниях частоты гамет являются произведениями частот соответствующих генов. Верно и обратное утверждение.

    Формальный нейрон Мак-Каллока - Питтса

    Модель отражает единственный атрибут биологического нейрона -его способность генерировать импульсы “все, или нечего” в ответ на достаточно сильное воздействие. Нейрон Мак-Каллока - Питтса функционирует в дискретном времени. Он имеет 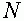Рефераты | Рефераты по математике | Математические модели в естествознании входов -синапсов и единственный выход. Значение выходного сигнала 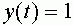Рефераты | Рефераты по математике | Математические модели в естествознаниисоответствует генерации спайка (состояние возбуждения). В состоянии покоя выходной сигнал 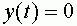Рефераты | Рефераты по математике | Математические модели в естествознании. В момент времени 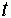Рефераты | Рефераты по математике | Математические модели в естествознании выходной сигнал формируется в зависимости от сигналов 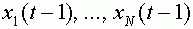Рефераты | Рефераты по математике | Математические модели в естествознании, поступивших на синапсы в момент времени 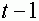Рефераты | Рефераты по математике | Математические модели в естествознании. Последние также могут принимать значения ноль или единица. Если синаптический сигнал равен нулю, то говорят, что синапс находится в состоянии покоя. Единичное значение соответствует состоянию возбуждения синапса. Сигнал на синапс поступает либо от выхода другого нейроны, либо от сенсора -специального входа для внешних сигналов. Первоначально правила формирования выходного сигнала были введены авторами модели в виде ряда аксиом. Приведем две из них.

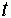    Для возбуждения нейрона в момент времени Рефераты | Рефераты по математике | Математические модели в естествознании необходимо в момент времени 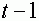Рефераты | Рефераты по математике | Математические модели в естествознании возбудить определенное, фиксированное число синапсов, которое не зависит ни от предыдущей истории, ни от состояния нейрона. Нейрон имеет особые входы -тормозящие синапсы. Возбуждение любого из них в момент времени 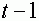Рефераты | Рефераты по математике | Математические модели в естествознании исключает возбуждение нейрона в момент времени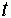 Рефераты | Рефераты по математике | Математические модели в естествознании

    Первая аксиома отражает пороговые свойства нейрона, а вторая - подчеркивает особую роль торможения (на сетях “без запретов” нельзя реализовать произвольный алгоритм).

    Впоследствии модель изменилась. Синаптические сигналы 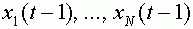Рефераты | Рефераты по математике | Математические модели в естествознании( не обязательно бинарные) стали взвешивать и формировать суммарный входной сигнал 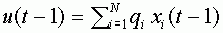Рефераты | Рефераты по математике | Математические модели в естествознании. Здесь 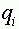Рефераты | Рефераты по математике | Математические модели в естествознании -числа, которые называют синаптическими весами. Синапс называют возбудительным, если 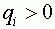Рефераты | Рефераты по математике | Математические модели в естествознании, и тормозным, если 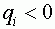Рефераты | Рефераты по математике | Математические модели в естествознании. Договорились, что в момент времени 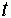Рефераты | Рефераты по математике | Математические модели в естествознании нейрон находится в возбужденном состоянии 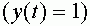Рефераты | Рефераты по математике | Математические модели в естествознании, если суммарный входной сигнал в момент времени 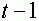Рефераты | Рефераты по математике | Математические модели в естествознании превысил некоторое пороговое значение 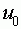Рефераты | Рефераты по мате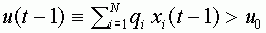матике | Математические модели в естествознании, т.е. Рефераты | Рефераты по математике | Математические модели в естествознании. Пусть 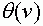Рефераты | Рефераты по математике | Математические модели в естествознании -функция Хевисайта. Она принимает нулевое значение при 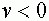Рефераты | Рефераты по математике | Математические модели в естествознании и единичное при 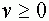Рефераты | Рефераты по математике | Математические модели в естествознании. Тогда можно записать:


    Рекомендуем скачать другие рефераты по теме: предмет курсовой работы, бесплатные рефераты и курсовые.



    Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 |




    Поделитесь этой записью или добавьте в закладки

       

    Категории:



    Разделы сайта




    •