
Метод изображений в электростатике
Категория реферата: Рефераты по математике
Теги реферата: пожары реферат, реферат
Добавил(а) на сайт: Platon.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Рефераты | Рефераты по математике | Метод изображений в электростатике |
q = - |
R d |
q. |
Таким образом, имеем систему двух точечных зарядов, расположенных так, как на рис. 7 .
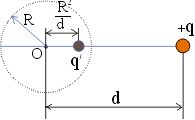
Рис. 7
На заряд +q со стороны сферы (или заряда-изображения q) действует сила притяжения
|
F = k |
q|q| (d-x)2 |
= k |
q2 d2-R2 |
. |
Mы рассмотрели случай заземленной проводящей сферы. А как быть в том случае, если сфера имеет заряд Q или несет ненулевой потенциал? Ответ на этот вопрос очень прост - в центр сферы нужно добавить еще один точечный заряд q, величину которого определим из условия эквипотенциальности сферы.
Рассмотрим незаряженную металлическую изолированную сферу и заряд +q, расположенный на расстоянии d от ее центра. Какая сила действует на заряд? Cфера останется незаряженной. Произойдет лишь перераспределение зарядов по поверхности сферы, связанное с взаимодействием с зарядом +q. Ближняя к заряду часть сферы приобретет отрицательный заряд, а дальняя - положительный, так как электроны притянутся к заряду (рис. 8 ).
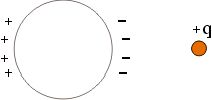
Рис. 8
Чтобы решить задачу, кроме заряда q, расположенного от центра сферы на расстоянии R2/d , в центре сферы надо расположить еще один заряд q (рис. 9 ).
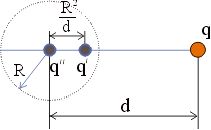
Рис. 9
Появление в центре сферы заряда q не меняет ее эквипотенциальности. Потенциал любой точки сферы создается теперь уже тремя зарядами - q, q и q. Суммарный потенциал, создаваемый зарядами q и q на поверхности сферы равен нулю, следовательно потенциал любой точки сферы определяется только зарядом q. Он равен = kq/R . Если сфера изолирована, то заряд q определится из условия
|
q+q = 0, q = |
R Рекомендуем скачать другие рефераты по теме: реферат личность, реферат отношения. Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |