Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

, если

, если

Элементы столбца матрицы будут элементами  в . Следовательно,

Мы определили миноры порядка  для  определителя. В общем случае, если из -матрицы выбросить все строки, кроме строк , и все столбцы, кроме столбцов , то определитель полученной в результате матрицы называется минором матрицы  порядка , то

Миноры, для которых , называются главными для матрицы . Если  -  матрица, то  и алгебраическое дополнение , например, есть

Если квадратная матрица является произведением некоторых матриц (которые могут быть прямоугольными), то иногда важно выразить определитель произведения в терминах свойств сомножителей. Следующая теорема - мощный результат этого рода.

§7 Теорема (формула Бине-Коши)

Теорема (формула Бине-Коши)

Пусть , -  и -матрицы соответственно, и

Тогда

Другими словами, при  определитель матрицы  является суммой произведений всевозможных миноров порядка  в  на соответствующие миноры матрицы  того же самого порядка.

Упражнение1. Покажем на примере

Пусть , , 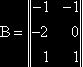 и , тогда по формуле Коши-Бине:

Доказательство теоремы:

Так как , то можно записать

Определитель-это аддитивная и однородная функция каждого из своих столбцов. Используя этот факт для каждого из  столбцов в , выражаем  в виде суммы  определителей:

Те члены в суммировании, которые имеют совпадающие два или более индексов , равны нулю, так как в этих случаях миноры будут иметь по крайней мере два совпадающих столбца. Таким образом, нужно рассматривать лишь те  членов суммирования, в которых индексы  различны. Мы распределяем эти остающиеся члены на  групп по  членов в каждой таким образом, чтобы в каждой группе члены отличаются лишь порядком индексов . Отметим также, что можно написать

, где . Следовательно, сумма по  членам, в которых -перестановка чисел , задается выражением:

Переставляя элементы  так, чтобы первые индексы в возрастающем порядке, приводим это выражение к виду:

где -перестановка  чисел , как очевидно . Из определителя функции определителя теперь следует, что это выражение есть просто:

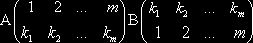
Следствие. Определитель произведения двух кратных матриц равен произведению определителй множителей.

Это следует из Теоремы при

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки