Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Лемма 1

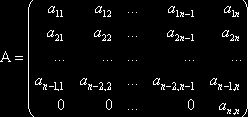и.

Доказательство:

 (в сумме только те слагаемые ненулевые, где )

Тогда подстановка имеет вид: , где . К подстановке  поставим в соответствие  т.е  

, такое соответствие называется взаимооднозначным отображением множества подстановок  на множество подстановок , . Очевидно, что и  имеют одинаковые инверсии, значит  имеют одинаковую четность и знаки

Лемма 2

Если равны нулю все элементы какой-либо строки (столбца) матрицы  за исключением быть может одного элемента, то определитель матрицы  равен произведению этого элемента на его алгебраическое дополнение

Доказательство:

Пусть все элементы -строки матрицы  за исключением элемента ,  перестановкой строк и столбцов  переместили элемент  в правый нижний угол , значит  строк и -столбцов. Знак будет меняться раз, после этого получиться матрица у которой все элементы последней строки кроме может быть  равны нулю. По Лемме 1 , т к

Теорема Лагранжа

 равна сумме произведений элементов какого-либо столбца (строки) матрицы  на их алгебраическое дополнение. Другими словами: разложение по -столбцу матрицы  имеет вид: , а разложение по -строке матрицы :

Доказательство:

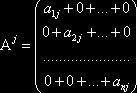рассмотрим -столбец матрицы  и запишем в виде: , по 6 свойству определителей:

, аналогично доказывается формула разложение по -строке матрицы .

Теорема 2

Справедливы равенства:

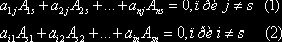
Рассмотрим матрицу , которая получена из матрицы  следующим образом: все столбцы матрицы , кроме -го такие же как и у матрицы . -тый столбец матрицы  совпадает с -столбцом , тогда у  два одинаковых столбца, поэтому определитель матрицы  равен нулю, разложим определитель матрицы  по -тому столбцу.

, , тогда . Формула (2) показывается аналогично.

Следствие:

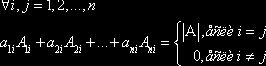
§5 Определитель произведение матриц

 поле скаляров, ,

Лемма 1

Рекомендуем скачать другие рефераты по теме: доклад 6 класс, здоровый образ жизни реферат.



Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки