Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата



tg a, cos 2a>0, поэтому последнее неравенство эквивалентно неравенству ctgk/2a–tgk/2a ³ k*cos 2a.

Положим f(a)=ctgna–tgna–2n*cos 2a, где n=k/2.

Далее, f/(a) = –(n/sin2a)ctgn-1a – (n/cos2a)tgn-1a + 4n*sin 2a = – n((ctgn-1a + tgn-1a) + (ctgn+1a + tgn+1a) – 4sin 2a) £ – n(2-2sin 2a)<0 при 0<a<p/4.

Здесь, как и в предыдущей задаче, использован тот факт, что сумма взаимно обратных положительных чисел больше или равна 2. Таким образом, на интервале 0<a<p/4 функция f убывает. В точке a=p/4 она непрерывна, поэтому (0; p/4] является промежутком убывания f. Наименьшим значением функции на этом промежутке является f(p/4)=0. Следовательно, f(a)³0 при 0<a<p/4. Для указанного промежутка неравенство доказано. Если p/4<a<p/2, то 0<p/2–a<p/4. Однако неравенство не меняется при заменен a на p/2–a. Задача 2 решена.

Задача 1.3. Что больше ep или pe ?

Решение.

0, b>0. Исключим тривиальный случай a=b и для определенности будем предполагать, что a<b. Ввиду симметричности вхождения a и b в уравнение, последнее замечание не ограничивает общности рассуждений. Ясно, что уравнение ab=ba равносильно уравнению b*(ln a)=a*(ln b), или

(ln a)/a = (ln b)/b.

Пусть f(x)=(ln x)/x  (1). Существование решений уравнения (1) эквивален-тно наличию значений x1 и x2 (x1<x2) таких, что f(x1)=f(x2). В этом случае пара (x1,x2) является решением уравнения (1). Иными словами, требуется выяснить, найдется ли прямая y=c, пересекающая график функции f по крайней мере в двух различных точках. Для этого исследуем функцию f. Ее производная f/(x)=(1–ln x)/x2 в области определения f имеет единственную критическую точку x=e. При 0<x<e f/(x)>0 функция f возрастает, а при x>e f/(x)<0 функция f убывает. Поэтому в точке x=e f принимает свое наибольшее значение (1/e). Так как функция (ln x)/x непрерывна и возрастает на промежутке (0,e], то она на этом промежутке принимает все значения от –¥ до 1/е. Аналогично, на промежутке [e,¥) функция f принимает все значения из (0,1/e]. Из результатов исследования функции f вытекают следующие утверждения:

1. Если 0<a<b и a£1, то (ln a)/a<(ln b)/b. Поэтому ab<ba . Следовательно, уравнение (1) и равносильное ему уравнение ab=ba не имеют решений.

2. Если 1<a<b£e, то ab<ba и уравнение ab=ba также не имеют решений.

3. Если b>a>e, то ab>ba.

Таким образом, если (a,b) является решением уравнения ab=ba , то 1<a<e, b>e. Более того, при каждом фиксированном значении 1<a<e найдется единственное значение b>e такое, что ab=ba

Для ответа на вопрос задачи 3 достаточно положить a=e, b=p и воспользоваться утверждением (1). Итак, ep > pe . Задача 3 решена.

Задача 1.4. Два туриста отправились по одному маршруту. В первый день они прошли одно и то же расстояние. В каждый из следующих дней первый турист увеличивал пройденный путь, по сравнению предыдущим, на одно и то же расстояние, а второй – в одно и то же число раз. Выяснилось, что в n-тый день (n>2) путешествия туристы снова прошли одно и то же расстояние. Доказать, что за n дней первый турист прошел путь больший, чем второй.

Решение.

Расстояние, пройденное первым туристом за n дней, представляет собой сумму n первых членов арифметической прогрессии, а вторым – сумму n первых членов геометрической прогрессии. Обозначим эти расстояния соответственно Sn и Sn/. Если a – первый член прогрессии, d – разность арифметической прогрессии, q – знаменатель геометрической прогрессии, то

  

Приравнивая n-е члены прогрессий, находим

 

Тогда  , где q>1 (по условию задачи). Задача 4 будет решена, если мы покажем, что , где n>2, q>1  (2)

При n=3 имеем , что равносильно очевидному неравенству . Предполагая, что неравенство (2) справедливо при n=k, докажем его для n=k+1. Имеем

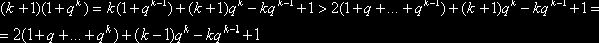
Для завершения доказательства достаточно убедиться, то выражение  при k>2. Здесь целесообразно обратиться к производной.

Пусть  Производная  положительная при x>1. Поэтому f при x>1 возрастает. Так как f(1)=0 и функция f непрерывна в точке x=1, то f(x)>0 при x>1, т.е. f(q)>0. Итак, Sn>Sn/. Задача 4 решена.

1.2. Использование основных теорем дифференциального исчисления при доказательстве неравенств

ТЕОРЕМА 1 (Ролля).Пусть функция f:[a,b]®R удовлетворяет условиям:

Рекомендуем скачать другие рефераты по теме: диплом управление, бесплатные тесты.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки