Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Решение.

Предварительно следует проверить соответствующее неравенство для производных левой и правой частей, т.е. что , или . Его справедливость при  можно установить, если применить теорему 1 к неравенству . Поскольку, кроме того, , то выполняются все условия теоремы 2. Поэтому имеет место строгое неравенство , , или 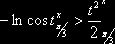, . После преобразований придем к неравенству (2.8).

2.3. Интегралы от выпуклых функций

При решении многих задач целесообразно применять следующий подход.

Разделим отрезок [a,b], на котором задана непрерывная функция f. на n частей точками . Построим прямоугольные трапеции, основаниями которых являются отрезки xkyk, xk+1yk+1, а высотами – xkxk+1, k=0,1,…,n-1. Сумма площадей этих трапеций при достаточно большом n близка к площади криволинейной трапеции. Чтобы этот факт можно было применить к доказательству неравенств функция f должна удовлетворять некоторым дополнительным требованиям.

Пусть функция f дважды дифференцируема на некотором промежутке и в каждой точке этого промежутка f//(x)>0. Это означает, что функция f/ возрастает, т.е. при движении вдоль кривой слева направо угол наклона касательной к графику возрастает. Иными словами, касательная поворачивается в направлении, обратном направлению вращения часовой стрелки. График при этом «изгибается вверх», «выпячиваясь вниз». Такая функция называется выпуклой. График выпуклой функции расположен «ниже» своих хорд и «выше» своих касательных. Аналогично, если f//(x)<0, то f/ убывает, касательная вращается по часовой стрелке и график лежит «выше» своих хорд, но «ниже» своих касательных. Такая функция называется вогнутой.

Функция  вогнута в области своего определения, так как . Вторая производная функции  положительна на всей числовой прямой. Поэтому  – выпуклая функция. Для функции  вторая производная  при ,  при , т.е. функция  на интервале

 вогнута, а на  выпукла.

Задача 2.7. Доказать, что

Решение.

Левая часть этого неравенства равна площади прямоугольной трапеции, основания которой равны значениям функции  в точках  и , т.е. и , а высота – . Функция  выпуклая. Поэтому площадь криволинейной трапеции, ограниченной ее графиком, прямыми  и отрезком [a,b] оси x, меньше площади прямоугольной трапеции. Итак,

.

Подобный результат имеет место и в общем случае. Пусть функция f на отрезке [a.b] непрерывна, положительна и выпукла. Тогда

                                       (2.9)

Если же непрерывная, положительная функция f вогнута, то

                                  (2.10)

Задача 2.8. Доказать, что для  выполняется неравенство

Решение.

Функция  непрерывна, положительна, вогнута. Поэтому для нее выполняется неравенство (2), где . Имеем

.

График функции f, выпуклой на отрезке [a,b] лежит выше любой касательной к этому графику, в частности касательной, проведенной через точку кривой с абсциссой .

Если касательная пересекает ось абсцисс вне отрезка [a,b], то она отсекает от криволинейной трапеции прямоугольную трапецию, а не треугольник. Площадь прямоугольной трапеции равна произведению ее средней линии  на высоту . Поэтому

                    (2.11)

аналогично, если функция f вогнута, то

                    (2.12)

Соотношение остается справедливым если касательная к графику  пересекает ось абсцисс в точках a и b.

Рекомендуем скачать другие рефераты по теме: диплом управление, бесплатные тесты.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки