Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

x = 2√5 R/15 _ _

Vпр.max = 2(4R2*2√5R/(5*15) – 2√5R*4R2/(45*5) - _ 40√5R3/(225*15)) = 16R3√5(1 – 1/3 – 5/45)/75 = 16√5R3/135.

Ответ: 16√5R3/135 м3 при H = 2√5R/15.

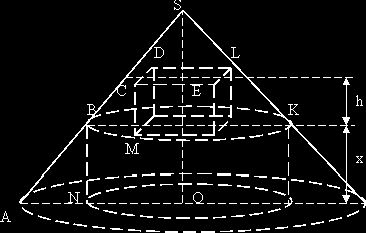
Задача 9. В конус вписан цилиндр, одно из оснований которого лежит в плоскости основания конуса, а окружность другого основания принадлежит боковой поверхности конуса. Правильная четырехугольная призма расположена так, что ее нижнее основание лежит в плоскости верхнего основания цилиндра, вершины верхнего основания принадлежат боковой поверхности конуса. Отношение длины диагонали основания призмы к ее высоте равно отношению длины диаметра цилиндра к его высоте. При какой высоте цилиндра объем призмы будет наибольшим? Найти этот объем призмы, если высота конуса – H и радиус основания – R.

Дано. ASO – конус;

SO = H;

AO = R;

CL/CM = BK/BN;

Найти. BN, чтобы Vпр = max

Решение. BN = x, CM = h, Vпр = Sосн CM = CL2h/2.

∆CSD подобен ∆ASO: CD/AO = SD/SO;

CD/R = (H – x - h)/H;

CD = R(H – x -h)/H.

∆BSE подобен ∆ASO: BE/AO = SE/SO;

BE/R = (H - h)/H;

BE = R(H - h)/H.

Находим отношение CD/BE = (H – x - h)/(H - x).

Исходя из условия (CL/CM = BK/BN) задачи делаем вывод,

что CD/BE = h/x, т. е. (H – x - h)/(H - x) = h/x => h = (Hx – x2)/H

Тогда CD = R(H – x – (Hx – x2)/H)/H = R(H2 – Hx – Hx +x2)/H2 = R(H - x)2/H2,

CL = 2CD = 2R(H - x)2/H2.

V = 4R2(H - x)4(H - x)x/(2H*H4) = 2R2(H - x)5x/H5;

V’(x) = 2R2((H - x)5 – 5(H - x)4 x)/H5 = 0,

(H – x) – 5x = 0, x = H/6.

V = 2HR2(5H/6)5/(6H5) = 2R2H*55/66.

Ответ: при H/6, Vmax = 2R2H*55/66.

В физике производная применяется в основном для вычисления наибольших или наименьших значений для каких-либо величин.

Задача 1.Потенциальная энергия U поля частицы, в котором находится другая, точно такая же частица имеет вид: U = a/r2 – b/r, где a и b — положительные постоянные, r — расстояние между частицами.

Найти:

а) значение r0 соответствующее равновесному положению частицы;

б) выяснить устойчиво ли это положение;

в) Fmax значение силы притяжения;

г) изобразить примерные графики зависимости U(r) и F(r).

U = a/r2 – b/r;  Решение:

a и b — counts;  Для определения r0 соответствующего равновесному

r0 — ?   положению частицы исследуем f = U(r) на экстремум.

Fmax — ?   Используя связь между потенциальной энергией поля

U и F, тогда F = -dU/dr, получим F = -dU/dr = - (-2a/r3+b/r2) = 0;

при этом r = r0; 2a/r3 = b/r2 => r0 = 2a/b;

Устойчивое или неустойчивое равновесие определим по знаку второй производной:

d2U/dr02= dF/dr0=-6a/r04 + 2b/r03 = -6a/(2a/b)4+2b/(2a/b)3=(-b4/8a3)<0;

равновесие устойчивое.

Для определения Fmax притяжения исследую на экстремумы функцию:

F = 2a/r3— b/r2;

dF/dr = -6a/r4 + 2b/ r3 = 0;

при r = r1 = 3a/b;

подставляя, получу Fmax = 2a/r31 — b/r31 = - b3/27a2;

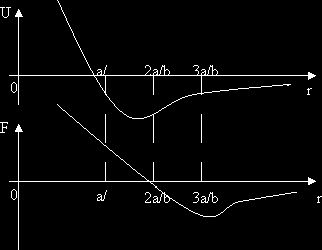U(r) = 0; при r = a/b; U(r)min при r = 2, a/b = r0;

F = 0; F(r)max при r = r1 = 3a/b;

Задача 2. Три резистора сопротивлениями R1, R2, R3 соединены параллельно. Сопротивление R1 в 9 раз больше сопротивления R2. Если все три резистора соединить последовательно, то сопротивление цепи равно R.

Рекомендуем скачать другие рефераты по теме: греция реферат, республика реферат.



Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки