Предыдущая страница реферата | 15  16  17  18  19  20  21  22  23  24  25 | Следующая страница реферата

	lim((1-cosx)/x) = lim((2sin2(x/2))/x) = lim((sin(x/2))*sin(x/2)/(x/2))=    x→0                                x→0                                                 x/2→0  =lim((sin(x/2))/(x/2))*lim(sin(x/2)) = 1*0 = 0        x/2→0                                                 x/2→0

т. е. 1—cos x при х → 0 есть бесконечно малая высшего порядка малости, чем х.

Дифференциал функции

1°. Определение. Дифференциалом (dy) функции y=f(x) называется произведение значения производной f '(х) на произвольное приращение ∆x аргумента х, т. е.

	dy=f '(x)*∆x

(I)

2°. Для получения значения дифференциала функции необходимо знать два числа: начальное значение аргумента, х, и его приращение, ∆x.

Пример. Вычислить дифференциал функции у = x2 при изменении значения аргумента х от 3 до 3,1.

Решение. dy=f '(х)* ∆х. Найдем dy сначала для произвольных значений х и ∆x.

f '(x) = (x2)' =2x.

Поэтому

dy=2x*∆x.

Начальное значение аргумента х=3, приращение его ∆x = 3,1 — 3 = 0,1. Подставляя эти значения в выражение dy находим:

dy =2*3*0,1=0,6.

Для данного значения независимого переменного х дифференциал функции f(x) есть линейная функция приращения независимого переменного ∆х.

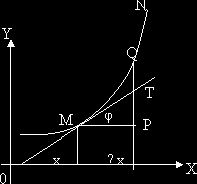
3°. Рассмотрим геометрический смысл дифференциала функции. На черт. в точке х проведена касательная к графику функции y=f(x). Из ∆MPT следует, что

PT = MP*tgφ = ∆x*f '(x).

Но по определению f '(х) *∆x = dy, поэтому PT = dy.

Дифференциал функции f(x) при данном значении х геометрически выражается приращением ординаты касательной к графику функции y=f(x) в точке х.

4°. Дифференциал dy и приращение ∆у вообще не равны между собой. На черт. dy = PT менее ∆y=PQ.

Рекомендуем скачать другие рефераты по теме: греция реферат, республика реферат.



Предыдущая страница реферата | 15  16  17  18  19  20  21  22  23  24  25 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки