Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата

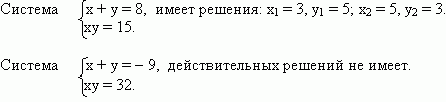
Ответ: x1 = 3, y1 = 5; x2 = 5, y2 = 3.

Пример 9.41. Решить систему

Решение. Сначала введём неизвестные X и Y:

X = 1 / x, Y = 1 / y,

а затем U и V: U = X + Y = 1 / x + 1 / y, V = XY = 1 / xy.

Получается система:

из которой U = 5, V = 6. Далее решая систему

находим X1 = 2, Y1 = 3; X2 = 3, Y2 = 2, откуда получаем x1 = 1 / 2, y1 = 1 / 3; x2 = 1 /3, y2 = 1 / 2. Можно сразу ввести неизвестные U = x + y, V = xy, получится система

Приводящая к тем же решениям исходной системы.

Ответ: x1 = 1 / 2, y1 = 1 / 3; x2 = 1 /3, y2 = 1 / 2.

Уравнения и системы уравнений с параметрами.

Иногда в уравнениях некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами. Такие буквы называются параметрами. Предполагается, что эти параметры могут принимать любые числовые значения, т.е. одно уравнения с параметрами задаёт множество уравнений (для всех возможных значений параметров).

Например, линейное уравнение ax + b = c с неизвестным x можно рассматривать как уравнение с параметрами a, b, и c. Его решением при a ¹ 0 является x = (c - b) / a. Если a = 0, то получается “уравнение” b = c, и если действительно b = c, то корнями данного уравнения являются все действительные числа. Если же b ¹ c, при этом a = 0, то данное уравнение корней не имеет.

Так, с параметрами учащиеся встречаются при введении некоторых понятий. Не приводя подробных определений, рассмотрим случай в качестве примеров следующие объекты:

функция прямая пропорциональность: y = kx (x и y — переменные; k — параметр,k ¹ 0); линейная функция: y = kx + b (x и у — переменные, k и b —параметры); линейное уравнение: ax + b = 0 (x — переменная; a и b —параметры); уравнение первой степени: ax + b = 0 (x — переменная; a и b — параметры, a ¹ 0); квадратное уравнение: ax2 + bx + c = 0 (x — переменная; a, b и c — параметры, a ¹ 0).

Решить уравнение с параметрами означает следующее:

исследовать, при каких значениях параметров уравнение имеет корни и сколько их при разных значениях параметров. Найти все выражения для корней и указать для каждого из них те значения параметров, при которых это выражение действительно определяет корень уравнения.

Ответ к задаче “решить уравнение с параметрами” должен выглядеть следующим образом: уравнение при таких- то значениях параметров имеет корни …, при таких- то значениях параметров — корни …, при остальных значениях параметров уравнение корней не имеет.

Пример 10.42. Решим уравнение px = 6 с неизвестным x и параметром p. Если p ¹ 0, то можно разделить обе части уравнения на p, и тогда мы находим корень уравнения x = 6 /p. Если p = 0, то уравнение корней не имеет, потому что 0× x = 0 для любого x.

Ответ: при p ¹ 0 уравнение имеет единственный корень x = 6 / p; при p = 0 уравнение корней не имеет.

Пример 10.43. Сравнить: - a и 3a.

Решение. Естественно рассмотреть три случая:

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.

Предыдущая страница реферата | 14  15  16  17  18  19  20  21  22  23  24 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки