Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата



(1 - a)x2 + (4,5 - a)x + 4 = 0.

Уравнение имеет единственное решение в том случае, когда дискриминант равен нулю:

(9 / 2 - a)2 - 4× 4(1 - a) = 0, т.е. a2 + 7a + 17 / 4 = 0, т.е. a = (- 7 ± 4Ö 2) / 2.

Ответ: a = 1, a = - 1 / 2, a = (- 7 ± 4Ö 2) / 2.

Пример 10.57.

x3 – (a + b + c)x2 + (ab + ac + bc)x – abc =0.

Решение. x3 – ax2 – bx2 – cx2 + abx + acx +bcx – abc = 0,

группируем: x2(x – a) – bx(x – a) – cx(x – a) – cx(x – a) + bc(x – a),

(x – a)(x2 – bc – cx + bc).

(x – a) = 0,

x1 = a.

x2 – bc – cx + bc = 0,

x(x – b) – c(x – b) = 0,

(x – b)(x – c) = 0,

x – b = 0, x2 = b

x – c = 0, x3 = c.

Ответ: x1 = a; x2 = b; x3 = c.

Замечание: корни уравнения можно было легко найти, пользуясь теоремой Виета для кубического уравнения:

если x3 + px2 + qx + r = 0, то

x1 + x2 + x3 = - p,

x1x2 + x1x3 + x2x3 = q,

x1x2x3 = - r .

В нашем случае:

x1 + x2 + x3 = a + b + c,

x1x2 + x1x3 + x2x3 = ab + bc +cd,

x1x2x3 = abc.

Отсюда следует, что x1 = a; x2 = b; x3 = c.

Графический метод решения систем нелинейных уравнений.

Системы нелинейных уравнений с двумя неизвестными можно решать графически. Для этого нужно начертить графики обоих уравнений и найти координаты точек их пересечения. Нам уже известны графики следующих уравнений:

ax + by + c = 0 — прямая линия. xy = k — гипербола. (x - a)2 + (y - b)2 = R2 — уравнение окружности с центром A(a, b) и радиусом R.

К этому виду приводятся с помощью выделения полных квадратов уравнения вида:

x2 + y2 - 2ax - 2by + c = 0.

ax2 + bx + c = 0 — парабола y = ax2 c вершиной в точке A(m, n), где m = - b / 2a, а n = (4ac - b2) / 4a.

Пример 11.58. Найдём графически корни системы:

Решение. Выделяя полные квадраты, получаем:

x2 + y2 - 2x + 4y - 20 = (x2 - 2x +1) + (y2 + 4y + 4) - 1 - 4 - 20 = (x - 1)2 + (y + 2)2 - 25.

Значит, систему уравнений можно записать так:

Графиком первого уравнения является окружность с центром A(1; - 2) и радиусом 5. А 2x - y = - 1 — уравнение прямой, проходящей через точки B(0; 1) и C(2; 5). Строим окружность радиуса 5 с центром в точке A и проводим прямую через точки B и C. Эти линии пересекаются в двух точках M(1; 3) и N(- 3; - 5). Значит решение системы таково: x1 = 1, y1 = 3; x2 = - 3, y2 = - 5.

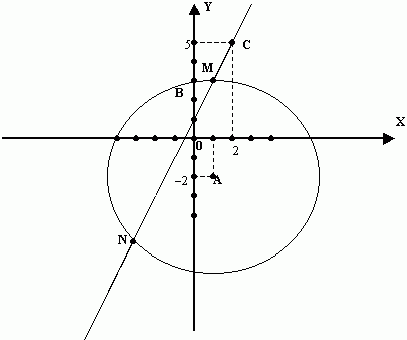Уравнения содержащие знак модуля.

Два числа, модули которых равны, либо равны между собой, либо отличаются лишь знаком: если | a| = | b| , то либо a = b, либо a = - b. Применим это замечание к решению уравнения

| 3x - 1| = | 2x + 3| .

В силу сказанного выше из этого уравнения вытекает, что либо 3х - 1 = 2х + 3, либо 3х - 1 = - (2х + 3). Корнем первого уравнения является число 4, а второго — число - 2 / 5. Итак, решение уравнения имеет вид х1 = 4, х2 = - 2 / 5.

В других случаях бывает полезно сначала установить, в каких точках обращаются в нуль выражения, стоящие под знаком модуля. Эти точки разбивают числовую ось на промежутки, внутри которых выражения сохраняют постоянный знак (промежутки знакопостоянства). Это позволяет освободиться на каждом из таких промежутков от знака модуля и свести задачу к решению нескольких уравнений — по одному на каждом промежутке.

При решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что

f (x), если f (x) ³ 0,

| f (x) | =– f (x), если f (x) < 0.

Пример 12.59. Решим уравнение.

| x| = | 3 - 2x| - x - 1.

Решение. Выражение x обращается в нуль при x = 0, а выражение 3 - 2x — при x = 3 / 2. Точки 0 и 3 / 2 разбивают числовую ось на промежутки (- ¥ ; 0),[0; 3 / 2], (3 / 2; ¥ ). При - ¥ < x < 0 имеем x < 0 и 3 - 2x > 0. Поэтому на этом промежутке | x| = - x, | 3 - 2x| = 3 - 2x и уравнение принимает вид - x = 3 - 2x - x - 1. Решая его, получаем, что x = 1. Но это значение x не лежит на (- ¥ ; 0), и потому на этом промежутке уравнение корней не имеет. При 0 £ x £ 3/ 2 имеем x ³ 0, 3 - 2x ³ 0, поэтому | x| = x, | 3 - 2x| = 3 - 2x. И уравнение принимает вид x = 3 - 2x - x - 1. Решая его, находим x = 0,5. Так как это значение x принадлежит промежутку [0; 3 / 2], то 1 / 2 является корнем заданного уравнения. Наконец, на промежутке (3 / 2; +¥ ) имеем x > 0, 3 - 2x < 0, а потому | x| = x, | 3 - 2x| = - (3 - 2x) и уравнение принимает вид x = - (3 - 2x) - x - 1, т.е. 0 = - 4. Значит, на этом промежутке нет корней заданного уравнения.

Мы получили, таким образом, что уравнение имеет лишь один корень, а именно x = 0,5.

Ответ: x = 0,5.

В некоторых случаях уравнение со знаком модуля имеет бесконечно много решений.

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.

Предыдущая страница реферата | 17  18  19  20  21  22  23  24  25  26  27 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки