Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата



Пример 12.60. | 8 - 5x| = | 3 + x| + | 5 - 6x| .

Выражения (8 - 5x), (3 + x) и (5 - 6x) обращаются в нуль соответственно в точках 8 /5, - 3, 5 / 6. Эти точки разбивают числовую ось на 4 промежутка. При этом, в ходе решения, устанавливаем, что на промежутках (- ¥ ; - 3), (5 / 6; 8 /5], (8 / 5; +¥ ) уравнение корней не имеет, а на промежутке [- 3; 5 / 6] оно обращается в тождество 8 - 5x = 3 + x + 5 - 6x. Поэтому ответ имеет вид [- 3; 5 / 6].

Ответ: [- 3; 5/ 6].

Несколько сложнее решаются уравнения, в которых встречается знак модуля под знаком модуля. Однако и в этом случае метод разбиения оси на промежутки знакопостоянства позволяет решить уравнение.

Пример 12.61. Решим уравнение | 2x - 3 - | x + 2| | = 8x + 12.

Решение. Выражение (x + 2) обращается в нуль при x = - 2. Если x < - 2, то (x + 2) < 0 и потому | x + 2| = - (x + 2). Значит, на промежутке (- ¥ ; - 2) заданное уравнение принимает вид | 2x - 3 + (x + 2)| = 8x + 12, т.е. | 3x - 1| = 8x + 12. Но при x < - 2 имеем 3x - 1 < 0 и потому | 3x - 1| = - (3x - 1). Получаем уравнение - (3x - 1) = 8x + 12, имеющее корень x = - 1. Так как это число не лежит на промежутке (- ¥ ; - 2), то заданное уравнение не имеет на это промежутке корней.

Пусть теперь x ³ - 2. Тогда | x + 2| = x + 2, и мы получаем уравнение | 2x - 3 - (x + 2)| =8x + 12, т.е. | x - 5| = 8x + 12. Здесь надо рассмотреть два случая: x < 5 и x ³ 5. В первом случае ½ x - 5| = - (х - 5), и потому получаем уравнение - (x - 5) = 8x + 12. Его корень равен - 7 / 9. Поскольку - 2 £ (- 7 / 9) £ 5, то - 7 / 9 является корнем заданного уравнения. Если же x ³ 5, то | x - 5| = x - 5 и уравнение принимает вид x - 5 = 8x + 12. Корнем полученного уравнения является число - 17 / 7. Поскольку оно не лежит на луче [5; +¥ ), оно не является корнем заданного уравнения. Итак, решение имеет вид x = - 7 / 9.

Ответ: x = - 7 / 9.

Пример 12.62.

| 1 – 2x| + | 3x + 2| + | x| = 5.

Решение. Приравниваем к нулю выражения, стоящие под знаком модуля, отмечаем на числовой оси полученные значения, исследуем уравнения в каждом из полученных интервалов:

А) если x < – 2 / 3, то 1 – 2x > 0, 3x + 2 < 0, x < 0 и уравнение переписывается так:

1 – 2x – 3x – 2 – x = 5, т.е. – 6x = 6, x = – 1 Î (–¥ ; – 2 / 3).

Б) если – 2 / 3 £ x < 0, то 1 – 2x > 0, 3x + 2 ³ 0, x < 0 и поэтому имеем:

1 – 2x + 3x + 2 – x = 5, и т.к. 3 ¹ 5, то в промежутке [– 2 / 3; 0) корней нет.

В) если 0 £ x < 0,5, то получаем: 1 – 2x + 3x + 2 + x = 5, т.е. 2x = 2; x = 1 Ï [0; 0,5).

Г) если 0,5 £ x, то – 1 +2x + 3x + 2 + x = 5, 6x = 4, x = 2 / 3 Î (0,5; ¥ ).

Ответ: x1 = – 1; x2 = 2 / 3.

Пример 12.63.

| x | + | x – 1 | = 1.

Решение. (x – 1) = 0, x = 1; Þ получаем интервалы:

A) x Î (- ¥ ; 0), тогда – x – x +1 = 1; – 2x = 0; x = 0 Ï (- ¥ ; 0).

Б) x Î [0; 1), тогда x – x +1 = 1; 1 = 1 Þ x — любое число из [0; 1).

В) x Î [1; ¥ ), тогда x + x – 1 = 1; 2x = 2; x = 1 Î [1; ¥ ).

Ответ: x Î [0; 1].

Основные методы решения рациональных уравнений.

1) Простейшие: решаются путём обычных упрощений — приведение к общему знаменателю, приведение подобных членов и так далее. Квадратные уравнения ax2 + bx + c = 0 решаются по выведенной нами формуле

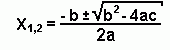
Также используется теорема Виета: x1 + x2 = – b / a; x1x2 = c / a.

2) Группировка: путём группировки слагаемых, применения формул сокращённого умножения привести (если удастся) уравнение к виду, когда слева записано произведение нескольких сомножителей, а справа — ноль. Затем приравниваем к нулю каждый из сомножителей.

3) Подстановка: ищем в уравнении некоторое повторяющееся выражение, которое обозначим новой переменной, тем самым упрощая вид уравнения. В некоторых случаях очевидно что удобно обозначить. Например, уравнение

(x2 + x – 5) / x + 3x / (x2 + x – 5) + 4 = 0,

легко решается с помощью подстановки (x2 + x – 5) / x = t, получаем t + (3 / t) + 4 = 0.

Или: 21 / (x2 – 4x + 10) – x2 + 4x = 6. Здесь можно сделать подстановку x2 – 4 = t. Тогда 21 / (t + 10) - t = 6 и т.д.

В более сложных случаях подстановка видна лишь после нескольких преобразований. Например, дано уравнение

(x2 + 2x)2 – (x +1)2 = 55.

Переписав его иначе, а именно (x2 + 2x)2 – (x2 + 2x + 1) = 55, сразу увидим подстановку x2 + 2x=t.

Имеем t2 – t – 56 = 0, t1 = – 7, t2 = 8. Осталось решить x2 + 2x = – 7 и x2 + 2x = 8.

В ряде других случаев удобную подстановку желательно знать “заранее”. Например

Уравнение (x + a)4 + (x + b)4 = c сводится к биквадратному, если сделать подстановку

x = t – (a + b) / 2.

Симметрическое уравнение (возвратное) a0xn + a1xn – 1 + … + a1x + a0 = 0 (коэффициенты членов, равностоящих от концов, равны) решается с помощью подстановки x + 1 / x = t, если n —чётное; если n — нечётное, то уравнение имеет корень x = – 1. Уравнение вида (x + a)(x + b)(x + c)(x + d) = l сводится к квадратному, если a + b = c + d и т.д.

4) Подбор: при решении уравнений высших степеней рациональные корни уравнения anxn + an – 1xn – 1 + … + a1x + a0 = 0 ищем в виде p / q, где p — делитель a0, q — делитель an, p и q взаимно просты, pÎ Z, qÎ N.

5) “Искусство”, т.е. решать пример нестандартно, придумать “свой метод”, догадаться что-то прибавить и отнять, выделить полный квадрат, на что-то разделить и умножить и т.д.

6) Уравнения с модулем: при решении уравнений с модулем используется определение модуля и метод интервалов. Напомним, что

f (x), если f (x) ³ 0,

| f (x) | =– f (x), если f (x) < 0.

Рациональные неравенства.

Пусть ¦ (c ) ¾ числовая функция одного или нескольких переменных (аргументов). Решить неравенство

¦ (c ) < 0 (¦ (c ) > 0) (1)

¾ это значит найти все значения аргумента (аргументов) функции ¦ , при которых неравенство (1) справедливо. Множество всех значении аргумента (аргументов) функции ¦ , при которых неравенство (1) справедливо, называется множеством решении неравенства или просто решением неравенства.

Множество решении нестрого неравенства

¦ (c ) £ 0(¦ (c ) ³ 0) (2)

представляет собой объединение множества решении неравенства (1) и множества решении уравнения ¦ (c ) = 0.

Рекомендуем скачать другие рефераты по теме: первый снег сочинение, научный журнал.

Предыдущая страница реферата | 18  19  20  21  22  23  24  25  26  27  28 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки