Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата



(АС/ВС)*(ВD/AD)=-1

3.7. Перспективные и проективные отображения.

Определение: Проективное отображение- это отображение прямой l на l' (быть может, совпадающую с l), которое, может быть представлено как композиция перспективных отображений.

Обозначение: l – l’ или АВС…-А’В’С’…

Последняя запись означает, что проективное отображение переводит точки А,В,С,….соответственно в A',B',C',….

Проективное отображение устанавливает взаимно однозначное соответствие между точками прямых l и l' и является отображением на l'.

Определение: Перспективным отображением прямой l на прямую l' (обе прямые рассматриваются как множество точек) с центром О (точка О не принадлежит ни l, ни l') называется отображение А® A', где для произвольной точки АÎ l точка А' находится как ОАÇ l'.

Обозначение l = l’ ("l переводится в l' перспективным отображением с центром в ()О". Отметим, что перспективное отображение устанавливает взаимно однозначное соответствие между точками l и l' и является отображением l на l' и что отображение, обратное перспективному отображению,

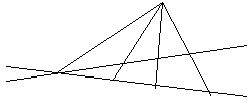
также является перспективным отображением. Если ()Х=lÇ l', то Х (как точка l) переходит в Х (как точку l'). Композиция двух или более перспективных отображений уже не обязательно будет перспективным отображением: так мы имеем l = l’ = l’’ и ABCY = A’B’C’Y’ = A’’B’’C’’Y’’ если бы полученное в результате композиции отображений l = l и l = l отображение l на l'’ было перспективным, то в точку lÇ l’'=Y оно должно было бы переводить в себя. Однако у переходит в точку Y'', которая не совпадает с Y. Поэтому мы ввели проективное отображение.

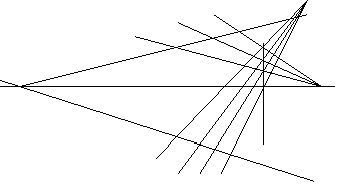
Предложение 1: Пусть, задана прямая l. Тогда множество проективных преобразований (взаимно однозначное отображение множества М на себя называется преобразованием множества М). l образует группу. Это означает, что 1)композиция двух проективных отображений снова есть проективное отображение. 2)отображение, обратное проективному отображению, снова есть проективное отображение.

Предложение 2: Пусть задана прямая l и пусть А,В,С и A',B',C'- две тройки ее различных точек. Тогда $ проективное преобразование l, переводящее А,В,С в A',B',C'.

Доказательство: Пусть l'- прямая отличная от l и не проходящая через А и А’, а О произвольная точка не принадлежащая ни l, ни l'. Спроектируем из О точки A',B',C' прямой l в точки A’’,B’’,C’’, прямой l’: A'B'C' = A''B''C'', где АÏ l’ и А’’Ï l.

Ясно, что нам достаточно построить проективное отображение l на l’, переводящее A,B,C, в A’’,B’’,C’’.

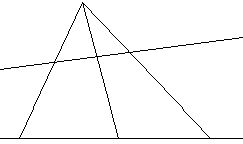
Заменим в обозначениях двойные штрихи одинарными и забудем про исходные A’,B’,C’. Таким образом, наша задача свелась к следующей. Заданы две различные прямые l и l’. Пусть А,В,С- три различные точки l, а A’,B’,C’-три различные точки l’, предположим что AÏ l’ и A’Ï l. Требуется построить проективное отображение l на l’, переводящее А,В,С соответственно в A’,B’,C’. Проведем прямые AA’,AB’,AC’,A’B,A’C и положим AB’Ç A’B=B’’, AC’Ç A’C=C’’. Обозначим прямую B’’C’’ через l’’; пусть она пересекает AA’ в A’’. Тогда l = l’’ = l’ переводит ABC = A’’B’’C’’ = A’B’C’.

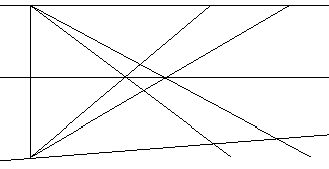
Таким образом, мы построили искомое проективное отображение l на l’ как композиция двух перспективных отображений.

Предложение 3: Проективное отображение переводит гармоническую четверку точек в гармоническую четверку.

3.8. Аксиома Паппа и основная теорема о проективных преобразованиях прямой.

Докажем “основную теорему”, которая утверждает, что существует единственное проективное преобразование прямой, переводящее три заданные точки в любые другие три заданные точки. Эта теорема не следует из аксиом П1-П5 и П7; поэтому нам предстоит дополнительно ввести аксиому Паппа П6.

Основная теорема (теорема о проективных преобразованиях прямой). Пусть задана прямая l и А,В,С;A’,B’,C’- две тройки различных точек этой прямой. Тогда существует одно и только одно проективное преобразование l, такое, что АВС - A’B’C’.

П6 (аксиома Паппа). Пусть l и l’-две различные прямые, А,В,С- три различные точки прямой l, отличные от Х=lÇ l’и А’,В’,С’- три различные точки прямой l’, отличные от Х. Тогда точки P=AB’Ç A’B, Q=AC’Ç A’C, R=BC’Ç B’C коллинеарны.

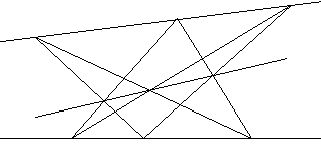
Предложение 1: Аксиома П6 влечет за собой двойственную аксиому Паппа П6*, то есть принцип двойственности применим и ко всем выводам из П6.

Предложение 2: На действительной проективной плоскости справедлива аксиома П6.

Лемма 1: Пусть l = m = n, где l¹ n, предположим еще, что или:

а)прямые l, m, n принадлежат одному пучку, или

б)точки O,P и lÇ n коллинеарны.

Тогда полученное проективное отображение l - n является перспективным (то есть $ такая точка Q, что перспективное отображение l = n совпадает с нашими проективными отображениями l - n).

Лемма 2: Пусть l = m = n,

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.

Предыдущая страница реферата | 9  10  11  12  13  14  15  16  17  18  19 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки