Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

П4. Каждая прямая плоскости А содержит хотя бы две точки. В S1 каждая прямая содержит несобственную точку. Следовательно прямая в S1 содержит не менее трех точек.

Все аксиомы проективной плоскости выполняются, следовательно, S1 - проективная плоскость.

3) Связка прямых евклидова трехмерного пространства - модель проективной плоскости, построенной на аксиомах П1-П4.

4) Действительная проективная плоскость (множество упорядоченных троек действительных чисел, одновременно не равных нулю), рассмотренная ранее, удовлетворяет аксиомам П1-П4.

3.4. Теорема Дезарга.

Одним из важных результатов проективной геометрии является теорема Дезарга, которая утверждает следующее:

П5 (теорема Дезарга)

Если прямые проходящие через соответственные вершины двух трехвершинников пересекаются в одной (), то () пересечения соответственных сторон этих трехвершинников лежат на одной прямой.

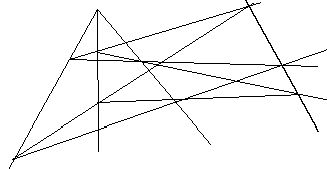
P=ABÇ A’B’AA’Ç BB’Ç CC’=0

Q=ACÇ A’C’

R=BCÇ B’C’

P,Q,R лежат на одной прямой.

В рамках теории, которую мы строим, не совсем правильно называть это утверждение “теоремой”, потому что нельзя доказать, исходя только из аксиом П1-П4. Примем это утверждение за аксиому П5. Хотя при первом и втором способе построения проективной плоскости это утверждение выступает как теорема.

Покажем, что П5 не есть следствие П1-П4, а именно, построим геометрию, удовлетворяющую аксиомам П1-П4, но не удовлетворяющую П5.

Определение: Конфигурацией называют множество элементов, именуемых точками, и набор его подмножеств, именуемых прямыми, если при этом выполняется аксиома.

К1. Две различные () принадлежат не более чем одной прямой.

Отсюда следует, что две различные прямые имеют не более одной общей точки

Примеры: Любая аффинная и " проективная плоскость являются конфигурациями. Набор 10 точек и 10 прямых теоремы Дезарга - тоже конфигурация.

Пусть p 0- некоторая конфигурация. Мы определим свободную проективную плоскость П, порожденную p 0.

Пусть p 1- новая конфигурация, определенная следующим образом. Точками p 1 являются точки p 0. Прямыми p 1 являются все прямые p 0; кроме того, каждая пара точек Р1, Р2Î p 0 не принадлежащая прямой из p 0, задает новую прямую

í Р1, Р2ý из p 1. Тогда p 1 обладает следующим свойством;

а) " две различные ()p 1 принадлежат одной прямой. Построим p 2, исходя из p 1, следующим образом. Точками p 2 служат все точки p 1; кроме того, каждая пара непересекающихся прямых l1,l2 задает новую точку l1Ç l2. Прямыми p 2 служат прямые p 1, пополненные новыми точками; например, () l1Ç l2 Î дополненным прямым l1 и l2. Тогда p 2 обладает следующим свойством.

б) " две различные прямые имеют общую точку; продолжим это построение. Для четных n мы построим p n+1 из p n, добавляя к прямым p n новые прямые; для нечетных n мы построим p n+1 из p n, добавляя к () p n новые точки.

Пусть теперь П= È p n

Элементы конфигураций p n мы назовем точками П; далее, прямой П мы назовем подмножество LÍ П, такое, что LÇ p n есть прямая из p n для всех достаточно больших n.

Предложение 1: Если p 0 содержит по меньшей мере четыре точки, никакие три из которых не принадлежат одной прямой, то П - проективная плоскость.

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.



Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки