Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

П2. " две прямые пересекаются по меньшей мере в одной точки.

П3. $ три неколлинеарные точки.

П4. Прямая содержит, по меньшей мере, три точки.

3.3. Модели проективной плоскости.

1)Рассмотренная ранее расширенная евклидовая плоскость есть модель проективной плоскости.

Доказательство: Проверим выполнение четырех аксиом П1-П4.

П1. Пусть P и Q Î

1. Если Р и Q - собственные (), то через них можно провести только одну прямую.

2. Если Р - собственная точка p , а Q- несобственная точка, то по аксиоме А2 $ прямая m, такая, что РÎ m и m || l, так , что Q Î пополнению прямой m до прямой из p . Прямая m -единственная прямая p , проходящая через Р и Q.

3. Если Р и Q несобственные (), то через них проходит единственная несобственная прямая.

П2. Пусть заданы прямые l и m.

1.Если l и m - несобственные прямые и l || m, то они пересекаются в некоторой точке. Если l || m, то они пересекаются в несобственной точке Р¥ .

2.Если l - собственная прямая, а m - несобственная прямая, то они пересекаются в несобственной точке Р¥ .

П3. Непосредственно следует из А3. Необходимо только проверить, что если Р и Q и R неколлинеарны в А, то они не будут коллинеарны в p . Действительно, в p $ только одна (несобсвтенная) прямая, не принадлежащая А, но () Р,Q,R ей не принадлежат.

П4. Каждая прямая плоскости А содержит хотя бы две (). Но в p каждая прямая содержит еще и несобственную точку, поэтому она содержит не менее трех точек.

2) Пополняя аффинную плоскость А из четырех (), мы получим проективную плоскость S1 из семи точек.

Докажем это: Проверим выполнение четырех аксиом П1-П4.

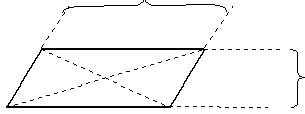
Определим () пересечения прямых АВÇ CD=N¥ , BCÇ AD=M¥ , АCÇ BC=P¥ N¥ , P¥ , M¥ Î одной несобственной прямой.

П1. Через две различные () плоскости можно провести единственную прямую.

Если А,В - собственные (), то через них можно провести только одну прямую из А. () А,В Î несобственной прямой, поэтому и в S1 через них можно провести единственную прямую.

Рассмотрим А- собственная () и N¥ - несобственная (). Через эти точки проходит единственная прямая, так как () N¥ определена как пересечение прямых АВ и CDÞ N¥ Î АВ.

Пусть имеем не собственные точки, через них проходит несобственная прямая S1 и она единственная.

П2. " две прямые пересекаются по меньшей мере в одной точке.

Справедливость аксиомы П2 следует из определения S1.

П3. $ три неколлинеарные точки.

Непосредственно следует из построения аффинной плоскости А. А мы дополнили точками N¥ , P¥ , M¥ (несобственными, которые принадлежат одной несобственной прямой). И поэтому точки не коллинеарные в А будут неколлинеарные в S1.

Рекомендуем скачать другие рефераты по теме: конспект урока 8 класс, шпаргалка егэ.



Предыдущая страница реферата | 5  6  7  8  9  10  11  12  13  14  15 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки