
Решение задач линейной оптимизации симплекс – методом
Категория реферата: Рефераты по математике
Теги реферата: реферат на тему животные, как сделать шпаргалку
Добавил(а) на сайт: Ефимия.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
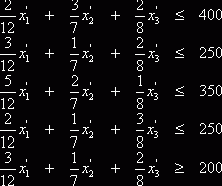 (2.5)
(2.5)
![]() , где
, где ![]() (2.6)
(2.6)
В канонической форме задачи линейного программирования необходимо, чтобы все компоненты искомого вектора Х были неотрицательными, а все остальные ограничения записывались в виде уравнений. Т.е. в задаче обязательно будут присутствовать условия вида (2.3) и 8 уравнений вида (2.2), обусловленных неравенствами (2.5), (2.6).
Число ограничений задачи, приводящих к уравнениям
(2.2) можно уменьшить, если перед приведением исходной задачи (2.4) - (2.6) к
канонической форме мы преобразуем неравенства (2.6) к виду (2.3). Для этого
перенесем свободные члены правых частей неравенств (2.6) в левые части. Таким
образом, от старых переменных ![]() перейдем к новым
переменным
перейдем к новым
переменным![]() , где
, где ![]() :
:
![]() ,
, ![]() .
.
Выразим теперь старые переменные через новые
![]() ,
, ![]() (2.7)
(2.7)
и подставим их в линейную форму (2.4) и в неравенства (2.5), (2.6). Получим
![]()
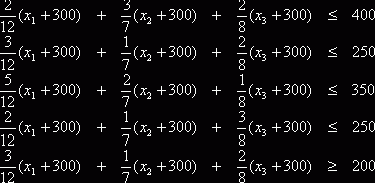
![]() , где
, где ![]() .
.
Раскрывая скобки и учитывая, что
![]() (2.8),
(2.8),
можем окончательно записать:
![]() (2.9)
(2.9)
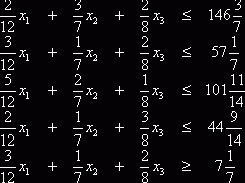 (2.10)
(2.10)
![]() , где
, где ![]() (2.11)
(2.11)
Путем несложных преобразований задачу (1.2.1), (1.2.2) свели к задаче (2.9) - (2.11) с меньшим числом ограничений.
Для записи неравенств (2.10) в виде уравнений введем
неотрицательные дополнительные переменные ![]() , и задача (2.9) - (2.11) запишется в следующей эквивалентной
форме:
, и задача (2.9) - (2.11) запишется в следующей эквивалентной
форме:
![]() (2.12)
(2.12)
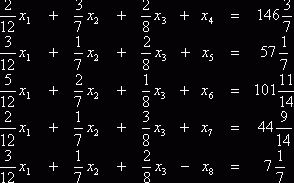 (2.13)
(2.13)
![]() , где
, где ![]()
Задача (2.12), (2.13) имеет каноническую форму.
3. Нахождение начального опорного плана с помощью L-задачи
Начальный опорный план задачи (2.1) - (2.3), записанной в канонической форме, достаточно легко может быть найден с помощью вспомогательной задачи (L-задачи):
Рекомендуем скачать другие рефераты по теме: доклад по географии на тему, реферат предприятие.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата