Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

                                                                                             (3.1)

                                                                         (3.2)

                                                                                       (3.3)

Начальный опорный план задачи (3.1) - (3.3) известен. Он состоит из компонент

                                                    

и имеет единичный базис Б = = E.

Решая вспомогательную задачу первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4), в силу ограниченности линейной формы сверху на множестве своих планов () получим, что процесс решения через конечное число шагов приведет к оптимальному опорному плану вспомогательной задачи.

Пусть - оптимальный опорный план вспомогательной задачи. Тогда  является опорным планом исходной задачи. Действительно, все дополнительные переменные . Значит, удовлетворяет условиям исходной задачи, т.е. является некоторым планом задачи (2.12) - (2.13). По построению план является также опорным.

3.1. Постановка L-задачи

Вспомогательная задача для нахождения начального опорного плана задачи (2.12) - (2.13) в канонической форме состоит в следующем.

Требуется обратить в максимум

при условиях

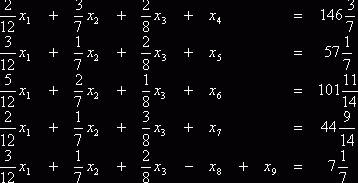
, где .

рассматривая в качестве исходного опорного плана план

Здесь добавление только одной дополнительной переменной  (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А4, А5, А6, А7.

3.2. Решение L-задачи

Решение L-задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4). Составим таблицу, соответствующую исходному опорному плану (0-й итерации).

Т.к. Б0 = - базис, соответствующий известному опорному плану, является единичной матрицей, то коэффициенты разложения векторов Аj по базису Б0

.

Значение линейной формы  и оценки  для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:

,

.

Отсюда получим:

Рекомендуем скачать другие рефераты по теме: доклад по географии на тему, реферат предприятие.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки