Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

где 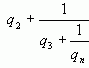>1, т.к.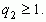

Поэтому и здесь 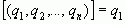. Докажем то, что рациональное число однозначно представляется цепной дробью 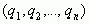, если .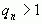

Пусть 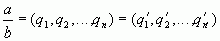с условием 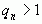, 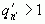. Тогда 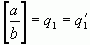, так что 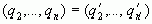. Повторным сравнением целых частей получаем 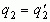, а следовательно 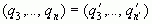и так далее. Если 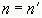, то в продолжении указанного процесса получим также 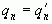. Если же 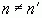, например 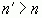, то получим 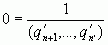, что невозможно.

Теорема доказана.

Вместе с тем мы установили, что при соблюдении условия 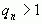между рациональными числами и конечными цепными дробями существует взаимно однозначное соответствие.

Замечания:

В случае разложения правильной положительной дроби первый элемент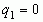 , например, 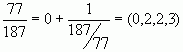. При разложении отрицательной дроби (отрицательный знак дроби всегда относится к числителю) первый элемент будет отрицательным, остальные положительными, так как целая часть отрицательной дроби является целым отрицательным числом, а ее дробная часть, как всегда, положительна.

Пример: 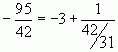, а так как 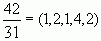, то .

Всякое целое число можно рассматривать как непрерывную дробь, состоящую из одного элемента.

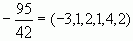Пример: 5=(5); .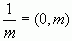

§2. Подходящие дроби. Их свойства.

Задаче разложения обыкновенной дроби в непрерывную дробь противостоит обратная задача – обращения или свертывания цепной дроби 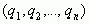в простую дробь .

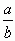При этом основную роль играют дроби вида:

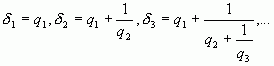или

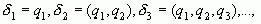которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа .

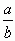Заметим, что 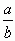==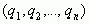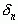. Считается, что подходящая дробь 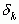имеет порядок k.

Прежде чем приступить к вычислению подходящих дробей заметим, что 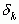переходит в 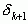, если в первой заменить 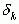выражением .

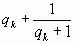Имеем ,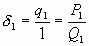

,

, …,

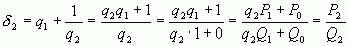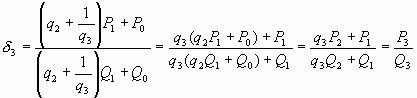при этом принимается, что 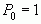, , 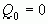, , 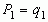, 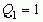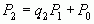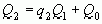и так далее.

Закономерность, которую мы замечаем в построении формулы для 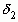(ее числителя 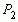и знаменателя 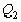), сохраняется при переходе к 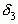и сохранится также при переходе от k к (k+1).

Поэтому, на основании принципа математической индукции, для любого k, где 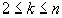, имеем

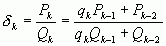(1),

причем 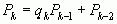(2)

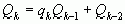(3)

Далее, говоря о подходящих дробях 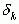(в свернутом виде), мы будем иметь в виду их форму .

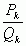Соотношения (1) являются рекуррентными формулами для вычисления подходящих дробей, а также их числителей и знаменателей. Из формул для числителя и знаменателя сразу видно, что при увеличении k они возрастают. Последовательное вычисление числителей 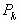и знаменателей 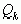подходящих дробей по формулам (2) и (3) удобно располагать по схеме:

Рекомендуем скачать другие рефераты по теме: курсовая работа по учету, дипломная работа по праву.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки