Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

;

.

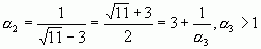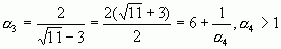Если остановиться на этом шаге, то можно записать:

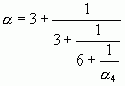
С другой стороны, из формулы для 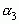видно, что 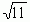=3+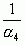. Поэтому 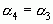, вследствие чего, начиная с этого момента, неполные частные станут повторяться.

Бесконечная непрерывная дробь, в которой определенная последовательность неполных частных, начиная с некоторого места, периодически повторяется, называется периодической непрерывной дробью.

Если, в частности, периодическое повторение начинается с первого звена, то цепная дробь называется чисто периодической, в противном случае – смешанной периодической.

Чисто периодическая дробь 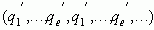записывается в виде 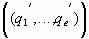, а смешанная периодическая 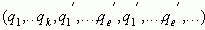в виде .

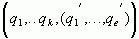Итак, 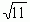разлагается в смешанную периодическую дробь (3, 3, 6, 3, 6, …) или (3, (3, 6)).

В общем случае разложения действительного иррационального числа 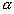поступаем так же, как в примере. Останавливаясь при этом в процессе выделения целой части после k–го шага, будем иметь:

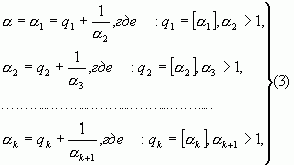
так что

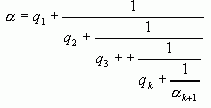
Числа 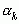называются остаточными числами порядка k разложения 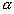. В формуле (4) имеем кусок разложения до остаточного числа .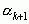

Для бесконечной цепной дроби (2) можно построить бесконечную последовательность конечных непрерывных дробей.

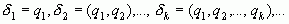
Эти дроби называют подходящими дробями. Закон образования соответствующих им простых дробей будет такой же, как и для подходящих дробей в случае конечных непрерывных дробей, так как этот закон зависит только от неполных частных 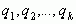и совершенно не зависит от того, является ли 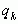последним элементом или за ним следует еще элемент 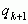. Поэтому для них сохранятся также остальные свойства, которые выводятся из закона образования числителей и знаменателей подходящих дробей.

В частности, мы имеем:

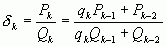, причем 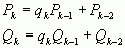; 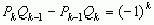, откуда следует несократимость подходящих дробей ; .

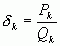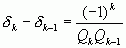Сравним теперь подходящую дробь 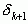и кусок разложения 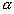до остаточного числа 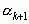. Имеем

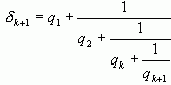
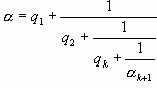
откуда видно, что вычисление 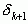по 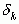формально производится таким же образом, как вычисление 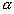по 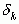с тем лишь отличием, что в первом случае 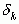заменяется на 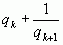, а во втором 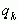заменяется на 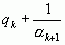. Поэтому на основании формулы 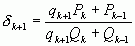можно сделать вывод о справедливости следующего важного соотношения

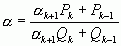. (5)

По этой причине мы пишем также 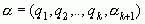, хотя 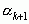не является здесь целым положительным числом.

При помощи формулы (5) можно вывести следующую теорему и расположении подходящих дробей разложения .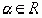

Теорема: Действительное число 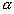всегда находится между двумя соседними подходящими дробями своего разложения, причем оно ближе к последующей, чем к предыдущей подходящей дроби.

Рекомендуем скачать другие рефераты по теме: курсовая работа по учету, дипломная работа по праву.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки