Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Соотношение 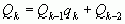(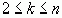) (*) показывает, что и все следующие знаменатели 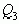, , 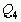…, 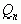положительны. При 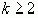, поскольку тогда 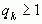, из (*) получаем

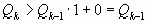, что и требовалось доказать.

Теорема: Нечетные подходящие дроби образуют возрастающую, а четные подходящие дроби – убывающую последовательность:

;

.

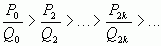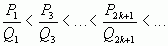Две подходящие дроб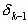и и 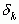, у которых номер отличается на единицу, будем называть соседними.

Теорема: Из двух соседних подходящих дробей четная дробь всегда больше нечетной.

Доказательство: По уже доказанному выше свойству имеем:

.

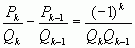Если k – четное, то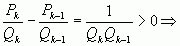

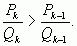
Если k – нечетное, то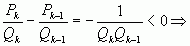

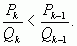
Значит, из двух соседних дробе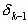й и 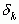четная всегда больше нечетной, что и требовалось доказать.

Теорема: Расстояние между двумя соседними подходящими дробями .

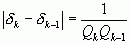Доказательство: Так как 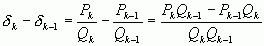, то 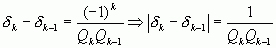, что и требовалось доказать.

Глава II. Бесконечные цепные дроби. §1. Представление действительных иррациональных чисел правильными бесконечными цепными дробями. Разложение действительного иррационального числа в правильную бесконечную цепную дробь.

В предыдущей главе мы рассмотрели, как в процессе последовательного выделения целой части и перевертывания дробной рациональная дробь разлагается в конечную непрерывную дробь.

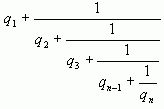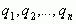=()(1)

и, наоборот, свертывание такой непрерывной дроби приводит к рациональной дроби.

Процесс выделения целой части и перевертывания дробной можно применить к любому действительному числу.

Для иррационального числа 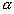указанный процесс должен быть бесконечным, так как конечная цепная дробь равна рациональному числу.

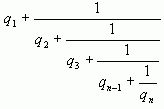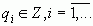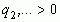Выражение (где , ) (2)

возникающее в таком процессе или заданное формально, мы будем называть правильной бесконечной цепной, или непрерывной дробью, или дробью бесконечной длины и обозначать кратко через (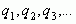), а числа 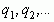– ее элементами или неполными частными.

Отметим, что разложение 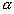возможно только в единственном виде, так как процесс выделения целой части – процесс однозначный.

Рассмотрим пример разложения иррационального числа .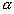

Пусть 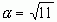. Выделим из 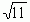его целую часть. 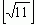=3, а дробную часть 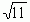–3, которая меньше 1, представим в ви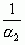де , где .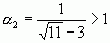

Повторяя операцию выделения целой части и перевертывания дробной, мы получаем:

;

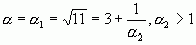Рекомендуем скачать другие рефераты по теме: курсовая работа по учету, дипломная работа по праву.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки