Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

где неполным частным последовательных делений 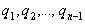соответствуют остатки 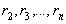с условием b>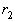>>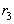…>>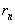0, а соответствует остаток 0.

Системе равенств (1) соответствует равносильная система

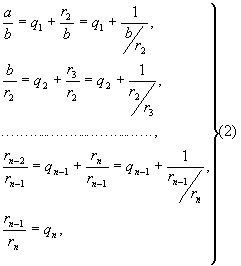
из которой последовательной заменой каждой из дробей 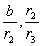и т.д. ее соответствующим выражением из следующей строки получается представление дроби 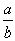в виде:

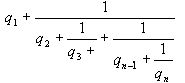
Такое выражение называется правильной (конечной) цепной или правильной непрерывной дробью, при этом предполагается, что 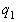– целое число, а 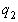, …, 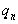- натуральные числа.

Имеются различные формы записи цепных дробей:

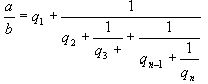
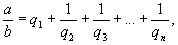
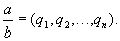
Согласно последнему обозначению имеем

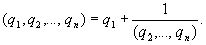
Числа 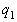, , 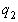…, 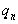называются элементами цепной дроби.

Алгоритм Евклида дает возможность найти представление (или разложение) любого рационального числа в виде цепной дроби. В качестве элементов цепной дроби получаются неполные частные последовательных делений в системе равенств (1), поэтому элементы цепной дроби называются также неполными частными. Кроме того, равенства системы (2) показывают, что процесс разложения в цепную дробь состоит в последовательном выделении целой части и перевертывании дробной части.

Последняя точка зрения является более общей по сравнению с первой, так как она применима к разложению в непрерывную дробь не только рационального, но и любого действительного числа.

Разложение рационального числа 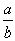имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деления a на b является конечным.

Понятно, что каждая цепная дробь представляет определенное рациональное число, то есть равна определенному рациональному числу. Но возникает вопрос, не имеются ли различные представления одного и того же рационального числа цепной дробью? Оказывается, что не имеются, если потребовать, чтобы было .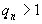

Теорема. Существует одна и только одна конечная цепная дробь, равная данному рациональному числу, но при условии, что .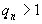

Доказательство: 1) Заметим, что при отказе от указанного условия единственность представления отпадает. В самом деле, при :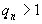

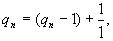
так что представление можно удлинить:

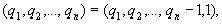
например, (2, 3, 1, 4, 2)=( 2, 3, 1, 4, 1, 1).

2) Принимая условие 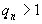, можно утверждать, что целая часть цепной дроби 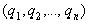равна ее первому неполному частному 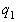. В самом деле:

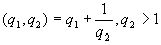если n=1, то если n=2, то ; поэтому 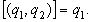если n>2, то

=

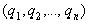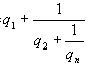
Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки