Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Из соотношения 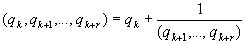получаем 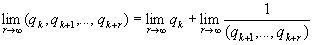, то есть 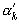= 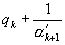(1).

Так как при 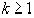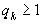, то все 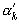>1, а 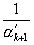<1; следовательно, 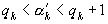, то есть 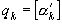(2). Но так как 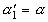, то 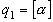и, ввиду равенства (1) 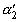равно остаточному числу второго порядка для , то есть 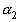. Тогда далее 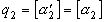, а 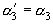и так далее. Вообще из 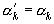следует 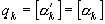, а .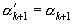

Элементы данной бесконечной непрерывной дроби получаются из его значения последовательным выделением целой части, что и требовалось доказать.

Вместе с тем мы установили, что остаток бесконечной непрерывной дроби = 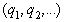порядка k+1 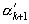совпадает с ее остаточным числом порядка k+1 .

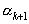Исследования этого параграфа приводят нас к следующему основному результату: каждое иррациональное действительное число единственным образом представляется бесконечной цепной дробью вида 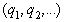и, наоборот, каждой бесконечной цепной дроби соответствует единственное иррациональное действительное число, которое она представляет. Поэтому множество всех действительных чисел взаимно однозначно отображается на множестве всех непрерывных дробей (если условиться, что для конечных непрерывных дробей берется последнее 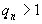). При этом рациональным числам соответствуют конечные непрерывные дроби, а иррациональным – бесконечные дроби.

§2. Приближение действительного числа рациональными дробями с заданным ограничением для знаменателя.

Рациональные числа образуют счетное множество, в то время как множество иррациональных чисел несчетно. В этом смысле можно сказать, что основную массу всех действительных чисел составляют иррациональные числа. Применение иррациональных чисел в практике обычно осуществляется заменой данного иррационального числа некоторым рациональным числом, мало отличающимся в пределах требуемой точности от этого иррационального числа. При этом обычно стараются выбрать рациональное число возможно простым, то есть в виде десятичной дроби с небольшим числом знаков после запятой или в виде обыкновенной дроби со сравнительно небольшим знаменателем.

Для громоздких рациональных чисел, то есть чисел с большими знаменателями, также иногда возникают задачи, связанные с необходимостью отыскания хороших рациональных приближений, понимая под этим отыскание рациональных чисел со сравнительно небольшими знаменателями, мало отличающимися от данных чисел.

Цепные дроби дают очень удобный аппарат для решения задач такого рода. С помощью цепных дробей удается заменять действительные числа рациональными дробями так, что ошибка от такой замены мала по сравнению со знаменателями этих рациональных чисел.

2.1. Оценка погрешности при замене действительного числа его подходящей дробью.

Теорема 1: Для любых двух соседних подходящих дробе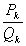й и 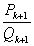к действительному числу имеет место неравенство 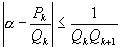, и если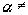 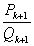, то .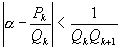

Доказательство: Если 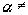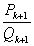, подходящие дроб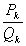и и 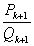, из которых одна четная, а другая – нечетная, лежат по разные стороны от (так как точное значение непрерывной дроби находится между двумя соседними подходящими дробями), и поэтому расстояние от до любой из них меньше длины интервала, образованного этими двумя подходящими дробями, то есть

.

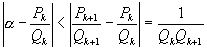Если =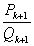, то .

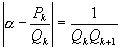Теорема 2: Для любой подходящей дроби 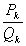к действительному числу справедливо неравенство:

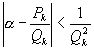
Доказательство: Если =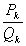, то получаем, что левая часть неравенства равна нулю, в то время как правая часть всегда больше нуля. Поэтому при = 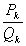неравенство выполняется. Пусть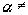 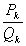, то есть существует подходящая дробь .

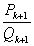При k>0 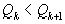и согласно предыдущей теореме имеем:

.

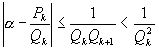Отдельно рассмотрим случай k=0. Если 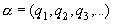, то

.

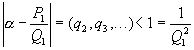Теорема 3: Если 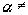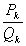, то .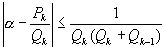

Из теорем 1-3 получаем следующие оценки погрешности:

, ,

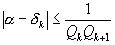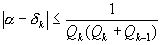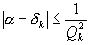
из которых первая является наиболее точной, а последняя – наиболее грубой.

2.2. Приближение действительного числа подходящими дробями.

Решение поставленной задачи начнем с рассмотрения нескольких примеров.

Пример 1: Рассмотрим задачу, аналогичную той, с которой встретился голландский математик Христиан Гюйгенс (1629-1695) при построении модели солнечной системы с помощью набора зубчатых колес и которая привела его к открытию ряда важных свойств непрерывных дробей.

Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.



Предыдущая страница реферата | 4  5  6  7  8  9  10  11  12  13  14 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки