Рефераты | Рефераты по математике | Теория цепных дробей Теория цепных дробей Категория реферата: Рефераты по математике Теги реферата: реферат суды, доклад Добавил(а) на сайт: Разуваев. Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата 3
	3	10	63	199
	1	3	19	60

Очевидно, нам достаточно взять 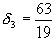, так как 19·60>1000. Это значение будет равно 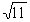с точностью до 0,001, причем с недостатком, так как 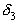– подходящая дробь нечетного порядка. Мы можем представить 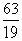в виде десятичной дроби, причем имеем право взять 3 знака после запятой, так как 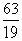является приближенным значением для 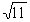с точностью до 0,001. Получаем 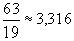(мы округляем по избытку, так как 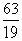является приближенным значением с недостатком, однако, не можем теперь сказать, будет ли 3,316 приближенным значением 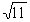с недостатком или избытком).

Решенные задачи в более общем виде формулируются так:

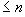Найти рациональное приближение к действительному со знаменателем в виде наиболее близкой к подходящей дроби. Для этого надо взять подходящую дробь для с наибольшим знаменателем, не превышающим n. Найти рациональное приближение к действительному числу с возможно меньшим знаменателем так, чтобы погрешность не превосходила 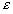(то есть с точностью до 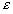). Для этого, пользуясь аппаратом цепных дробей, находим подходящую дробь 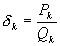с наименьшим знаменателем 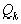так, чтобы 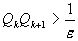. 2.3. Теорема Дирихле.

Выше мы нашли оценку погрешности, возникающей при замене любого действительного числа рациональными дробями определенного типа, а именно: подходящими дробями.

А сейчас рассмотрим некоторые сравнительно простые результаты, показывающие как обстоит дело с приближением действительных чисел рациональными числами, не предрешая заранее, что эти рациональные числа будут подходящими дробями.

Пусть – произвольное действительное число. Из теории десятичных дробей следует существование рационального числа 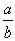такого, что 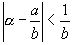. поставим вопрос о возможности таких приближений рациональными числами 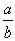, при которых точность приближения будет оценена не величиной 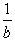, а величиной, в 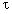раз меньшей, то есть вопрос о нахождении рациональных чисел 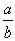таких, что 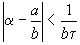, где 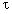– любое заранее положительное число.

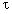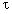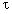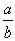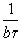Например, можно поставить задачу нахождения такого рационального приближения к , чтобы точность приближения была в 1000 или в 1000000 раз лучшей, чем величина, обратная знаменателю. Это соответствует выбору =1000 или =1000000. оказывается, что как бы велико ни было , можно найти рациональную дробь , приближающую с точностью до , причем и это является самым интересным, дробь 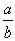мы можем выбрать так, что .

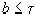Теорема Дирихле: Пусть и 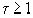– действительные числа; существует несократимая дробь 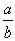, для которой ,

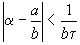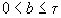
(или: существует такая пара взаимно простых целых чисел a и b, что , ).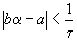

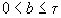Доказательство: Теорему легко доказать с помощью аппарата цепных дробей.

Пусть 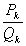подходящая дробь числа ; выберем наибольший из знаменателей 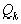, не превышающий 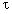, то есть наибольшее k, чтобы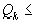 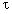и положим 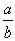=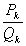. Рассмотрим два случая:

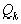не является последним знаменателем, то есть существует 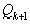такое, что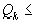 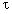<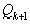. Тогда при a= 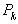и b=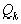 имеем:

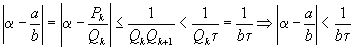
2) 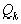– знаменатель последней подходящей дроби разложения , то есть =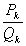. Тогда при a=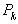, b=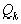, имеем:

.

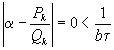Теорема доказана.

Сам Дирихле дал другое доказательство, использовав в нем принцип, который носит теперь имя Дирихле: при распределении N объектов между N-1 ящиками хотя бы в одном ящике должно находиться 2 объекта. Приведем это доказательство.

Пусть 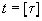, рассмотрим совокупность t+2 чисел, состоящую из 1 и значений дробных частей 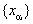для x=0, 1, …, t (причем 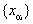=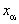-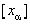, 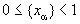). Очевидно, каждое из чисел этой совокупности принадлежит точно одному из t+1 промежутков 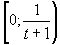, , 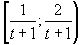…, , 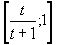из которых первые t являются полусегментами, а последний сегментом.

Так как чисел у нас t+2, то (согласно принципу Дирихле) обязательно найдется такой промежуток, который содержит 2 числа из совокупности 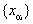и 1. Разность этих двух чисел не превосходит длину содержащего их промежутка, то есть .

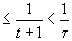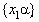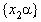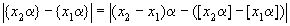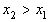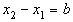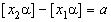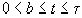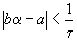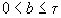Если такими числами являются и , то . Пусть и , . Так как , то , ). Если 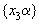и 1 принадлежат одному промежутку, то

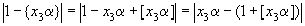
Пусть в таком случае 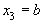, 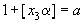. Очевидно, и здесь 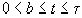, так что , ).

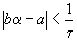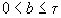Теорема доказана.

Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.



Предыдущая страница реферата | 6  7  8  9  10  11  12  13  14  15  16 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки