
Теория цепных дробей
Категория реферата: Рефераты по математике
Теги реферата: реферат суды, доклад
Добавил(а) на сайт: Разуваев.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата
Доказательство: Докажем первую часть. Разложим
 в цепную дробь. Мы докажем, что из трех любых соседних подходящих дробей
в цепную дробь. Мы докажем, что из трех любых соседних подходящих дробей 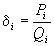 , i=k, k+1, k+2 по крайней мере одна удовлетворяет условию
, i=k, k+1, k+2 по крайней мере одна удовлетворяет условию 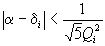 . Доказательство этого утверждения будем вести методом от противного. Предположим, что для каких-либо трех соседних подходящих дробей выполняются неравенства:
. Доказательство этого утверждения будем вести методом от противного. Предположим, что для каких-либо трех соседних подходящих дробей выполняются неравенства:
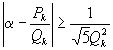 ,
, 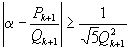 ,
, 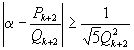 (2)
(2)
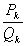 и
и 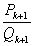 расположены по разные стороны от
расположены по разные стороны от  и поэтому при нечетном k из (2) следует
и поэтому при нечетном k из (2) следует
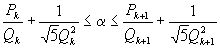 ,
,
а при четном: 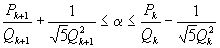 , так что и в том, и в другом случае имеем:
, так что и в том, и в другом случае имеем: 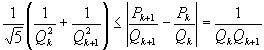
, или, умножая на 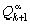 и перенося все члены в одну сторону
и перенося все члены в одну сторону 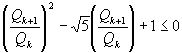 , то есть
, то есть 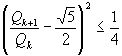 ,
, 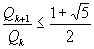 , или, поскольку
, или, поскольку 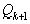 и
и 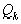 целые,
целые, 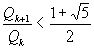 . (3)
. (3)
Так как 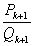 и
и 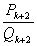 также расположены по разные стороны от
также расположены по разные стороны от  , из (2) аналогично получаем:
, из (2) аналогично получаем: 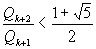 . (4)
. (4)
Пользуясь еще тем, что 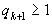 из (3) и (4) получаем:
из (3) и (4) получаем:
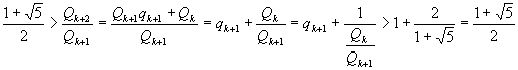 .
.
Предположение, что выполнены все три неравенства (2), привело нас к противоречию, поэтому по крайней мере для одной из трех подходящих дробей 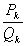 ,
, 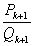 ,
, 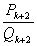 , взятой в качестве
, взятой в качестве 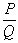 , должно выполняться неравенство (
, должно выполняться неравенство (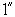 ).
).
Придавая k различные значения, получим бесконечное множество дробей, удовлетворяющих неравенству (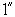 ).
).
Докажем вторую часть.
Предположим, что при 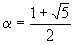 ,
, 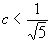 неравенство (1)
неравенство (1) 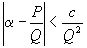 удовлетворяется для бесконечного множества рациональных чисел
удовлетворяется для бесконечного множества рациональных чисел 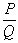 . Тогда для каждой такой дроби неравенства
. Тогда для каждой такой дроби неравенства 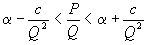 , откуда, подставляя значение
, откуда, подставляя значение  , получаем
, получаем 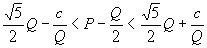 , а возводя в квадрат, получаем:
, а возводя в квадрат, получаем: 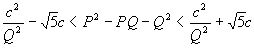 . Так как
. Так как 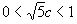 , то при достаточно большом Q будем иметь:
, то при достаточно большом Q будем иметь: 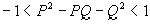 и, следовательно, целое число
и, следовательно, целое число 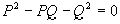 ,
, 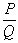 =
=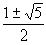 , что при целых P и Q не может иметь места. Полученное противоречие показывает, что неравенство (1) может иметь место только для конечного числа рациональных чисел
, что при целых P и Q не может иметь места. Полученное противоречие показывает, что неравенство (1) может иметь место только для конечного числа рациональных чисел 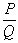 . Теорема доказана полностью.
. Теорема доказана полностью.
Эта теорема была опубликована Гурвицем в 1891 году. Тот факт, что из трех соседних подходящих дробей по крайней мере одна даст приближение вида 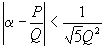 , был доказан Борелем в 1903 году.
, был доказан Борелем в 1903 году.
Последним теоремам можно дать и другое очень важное истолкование.
Рассмотрим для этого уравнение 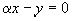 , где
, где  – любое действительное иррациональное число. Исключая тривиальное решение x=y=0, это уравнение не может иметь решение в целых числах. Однако можно поставить задачу о приближенном его решении в целых числах, то есть о нахождении таких пар чисел x(x>0) и y, чтобы:
– любое действительное иррациональное число. Исключая тривиальное решение x=y=0, это уравнение не может иметь решение в целых числах. Однако можно поставить задачу о приближенном его решении в целых числах, то есть о нахождении таких пар чисел x(x>0) и y, чтобы:
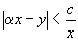 или
или 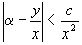 .
.
Теорема Гурвица-Бореля показывает, что для 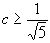 всегда существует бесконечное множество таких пар; если же
всегда существует бесконечное множество таких пар; если же 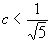 , то существуют такие действительные числа, для которых таких пар имеется лишь конечное множество.
, то существуют такие действительные числа, для которых таких пар имеется лишь конечное множество.
Новая точка зрения получает в содружестве с методом Дирихле весьма значительное применение в теории диофантовых приближений.
§ 3. Квадратические иррациональности и периодические цепные дроби.Рациональные числа представляют собой корни уравнений первой степени вида 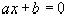 с целыми коэффициентами.
с целыми коэффициентами.
Во множестве иррациональных чисел наиболее простыми являются те иррациональности, которые являются корнями квадратных уравнений с целыми коэффициентами; такие числа будем называть квадратическими иррациональностями.
Число  называется квадратической иррациональностью, если
называется квадратической иррациональностью, если  – иррациональный корень некоторого уравнения
– иррациональный корень некоторого уравнения 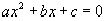 (1) с целыми коэффициентами, не равными одновременно нулю.
(1) с целыми коэффициентами, не равными одновременно нулю.
При таком  , очевидно, будет a
, очевидно, будет a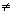 0, c
0, c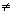 0. Коэффициенты a, b, c уравнения (1), очевидно, можно взять взаимно простыми; в этом случае дискриминант этого уравнения
0. Коэффициенты a, b, c уравнения (1), очевидно, можно взять взаимно простыми; в этом случае дискриминант этого уравнения 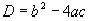 будем называть также дискриминантом
будем называть также дискриминантом  . Корни уравнения (1) равны
. Корни уравнения (1) равны 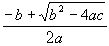 и
и 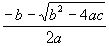 , так что любую квадратическую иррациональность
, так что любую квадратическую иррациональность  можно представить в виде
можно представить в виде 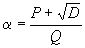 , где P, Q – целые, а D (D>1) – целое неквадратное число.
, где P, Q – целые, а D (D>1) – целое неквадратное число.
Второй корень уравнения (1) 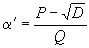 будем называть иррационал
будем называть иррационал ьностью,
сопряженной с .
ьностью,
сопряженной с .
В определении квадратической иррациональности особенно важно обратить внимание на то, что речь идет о квадратных уравнениях с целыми коэффициентами. Любое  является корнем квадратного уравнения и даже уравнения первой степени, например уравнений
является корнем квадратного уравнения и даже уравнения первой степени, например уравнений 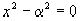 , x-
, x- =0.
=0.
Рекомендуем скачать другие рефераты по теме: таможенные рефераты, изложение по русскому языку 7.
Предыдущая страница реферата | 6 7 8 9 10 11 12 13 14 15 16 | Следующая страница реферата