Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата



5.Пример задачи для формулы полной вероятности.

Задача 5.1.

Пусть имеем три урны с шарами. В первой урне 7 белых и 3 черных шара. Во второй урне 7 белых и 7 черных шаров. В третьей урне 3 белых и 7 черных шаров. Наугад выбрали одну урну. Из этой урны наугад вынули шар.

Какова вероятность, что вынули белый шар?

Решение:

Пусть событие А – вынули белый шар, событие Ei – вынули шар из i-той урны, i=1,2,3. Вероятности P(Ei) полагаем равными, т.е. Р(Ei)=1/3. Вероятность Р(A|E1)=7/10, вероятность Р(А|E2)=7/14=1/2, вероятность Р(А|E3)=3/10. Таким образом по формуле полной вероятности (4.3) имеем

Р(А)=Р(A|E1)·Р(E1)+Р(A|E2)·Р(E2)+Р(A|E3)·Р(E3)=

=(1/3)·(7/10+5/10+3/10)=(1/3)·15/10=1/2(5.1)

Ответ:Вероятность вынуть белый шар равна Ѕ.

6.Пример задачи для формулы Бейеса.

Задача 6.1.

Пусть имеем те же урны с теми же наборами шаров, как и в задаче (5.1). Снова из выбранной наугад урны выбрали наугад шар. Оказалось, что вынули черный шар.

Какова вероятность, что его вынули из третьей урны?

Решение:

Пусть В – событие, состоящее в том, что вынули черный шар. События Ei те же, что и в решении задачи (5.1). Интересующая нас вероятность есть условная вероятность Р(E3|B). По формуле Бейеса (4.5) имеем

Р(Е3|B)=P(B|E3)·P(E3)/(P(B|E1)·P(E1)+P(B|E2)·P(E2)+P(B|E3)·P(E3)) (6.1)

У нас: Р(Ei)=1/3, i=1,2,3, P(B|E1)=3/10, P(B|E2)=1/2, P(B|E3)=7/10. Таким образом, получаем

Р(Е3|B)=(7/10)·(1/3)/((1/3)·(7/10+5/10+3/10))=(7/10)/(15/10)=7/15 (6.2)

Ответ:Вероятность того, что вынули шар из третьей урны, при условии, что шар оказался черным равна 7/15.

7.Геометрические вероятности.

Как сказано выше, вычисление вероятности на основе несовместимых равновозможных событий по формуле (2.1) называют обычно классическим определением вероятности. Однако применяют и другие способы вычисления вероятностей. Рассмотрим здесь геометрический способ вычисления вероятностей. При этом способе случайные события трактуются, как такие события, которые осуществляются, когда случайная точка попадает в ту или иную область на некоторой прямой или на плоскости или в пространстве. Поясним это подробнее на примере плоскости.

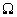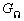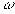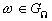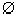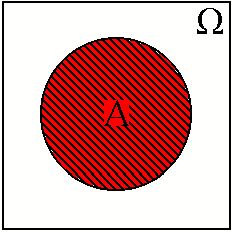
Достоверное событие представляется некоторой областью на плоскости. При этом полагается, что случайная точка обязательно попадает в эту область, т.е. обязательно . Невозможное событие представляется пустым множеством точек, т.е. таким множеством точек, которое не содержит ни одной точки. Т.е. случайная точка 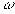никак не может оказаться точкой из этого пустого множества. Каждое случайное событие А из рассматриваемой алгебры событий L представляется некоторой областью 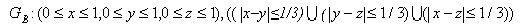, т.е. областью 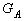, которая содержится в области 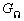. Случайное событие А осуществляется тогда и только тогда, когда случайная точка 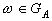, т.е. 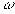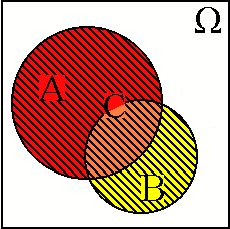тогда и только тогда, когда точка попадает в область 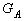. При такой трактовке объединение событий 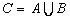представляется областью 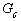, которая складывается из точек, каждая из которых лежит хотя бы в одной из областе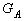й и 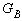. 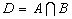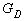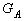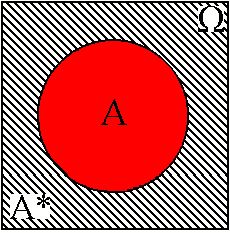Пересечение событий представляется областью , которая является общей частью областей и 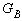. Противоположное событие А* представляется областью 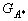, которая является дополнением к области 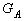до области 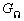. См. например фиг.7.1.-7.4.

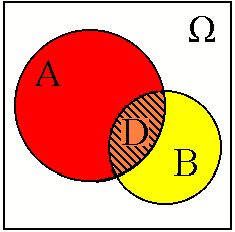
Фиг.7.1.
Фиг. 7.2.

Фиг.7.3.

Фиг. 7.4

Предполагая, что для каждой области 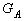при любом событии А из алгебры событий L можно определить площадь S 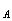этой области полагают вероятность события А равной

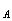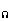Р(А)=S/S(7.1)

Смысл этого определения состоит в том, что для шансов попадания случайной точки 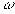в ту или иную точку из области 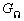не отдается никакого предпочтения.

Например, пусть область 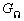есть квадрат со стороной единица. Событие А состоит в том, что случайная точка 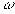попадает в четверть круга 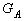с радиусом, равным единице, и вписанного в квадрат . См. фиг.7.5.

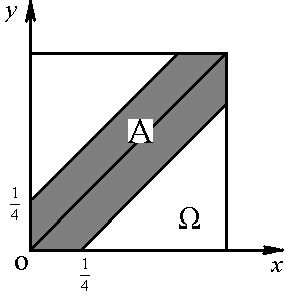
Фиг.7.5.

Тогда по формуле (7.1) получаем

Рекомендуем скачать другие рефераты по теме: российская федерация реферат, антикризисное управление предприятием.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки