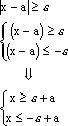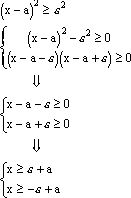
Теория вероятности и математическая статистика
Категория реферата: Рефераты по математике
Теги реферата: рефераты бесплатно скачать, наука реферат
Добавил(а) на сайт: Казнов.
Предыдущая страница реферата | 16 17 18 19 20 21 22 23 24 25 26 | Следующая страница реферата
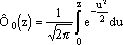
Свойства:
1) при z>0 функция Лапласа определяет вероятность попадания нормальной случайной величины с параметрами
MX=0
DX=1
в интервале (0, z)
2)
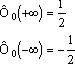
3) ![]() - функция нечетная
- функция нечетная
Иногда в литературе встречаются два вида функций Лапласа
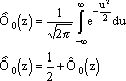
Функция Лапласа табулирована. Функция Лапласа используется для выполнения событий вида
![]()
для произвольных нормальных величин.
Найдем вероятность того, что в результате испытания над x произойдет сложное событие: x примет числовое значение, принадлежащее отрезку с концами (a, b).
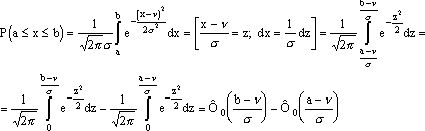
Пример.
x - случайная величина.
f(x) - плотность вероятности.
Найти плотность вероятности g(n) случайной величины H.

Рассмотрим отрезок (h, h+dh). Событию попадание H в отрезок (h, h+dh) в силу однозначности функции h(x) соответствует попадание x в отрезок (x, x+dx). При этом вероятности наступления такого события одинаковы:
![]()
Тогда построим функцию h(x), обратную x(h), x=x(h).
т.к. ![]()
Вероятность первого события равна
![]()
Вероятность второго события
![]()
Следовательно
![]()
Неравенство Чебышева
Рассмотрим
случайную величину X с конечным мат. ожиданием и дисперсией ![]()
Для любого неотрицательного числа t вероятность наступления события
![]()
Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ¥). Тогда имеет место неравенство
![]()
Доказать неравенства
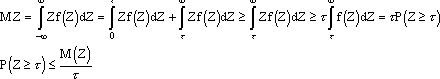
Рассмотрим два сложных события
![]()
a - произвольное действительное число.
Показать самим, что x - удовлетворяет и одному и другому неравенству.
Тогда ![]() справедливо
справедливо
![]()
В данном случае
![]()
Равномерность неравенств при e>0
|
|
|
или, в частности, при a=n=MX
Рекомендуем скачать другие рефераты по теме: bestreferat, quality assurance design patterns системный анализ.
Предыдущая страница реферата | 16 17 18 19 20 21 22 23 24 25 26 | Следующая страница реферата