Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

A) Пример.

Вычислим объем шара радиуса R. В этом случае подынтегральную функцию надо взять равной 1, и мы получим

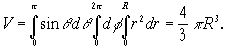
Применение тройных интегралов.

Для вычисления координат центра тяжести тела нужны статические моменты относительно координатных плоскостей Оху, Охz, Оуz; обозначим их соответственно Повторяя рассуждения получим следующие формулы для координат центра тяжести неоднородного тела, плотность которого задается функцией занимающего область :

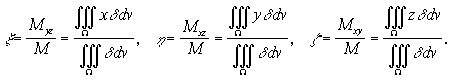
Если тело однородно, т. е. , то формулы упрощаются:

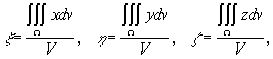
где V- объём тела.

Пример. Найдем центр тяжести однородного полушара :

Две координаты центра тяжести равны нулю, ибо полушар симметричен относительно оси Оz (тело вращения с осью Оz).

Интеграл удобно вычислить, перейдя к сферическим координатам:

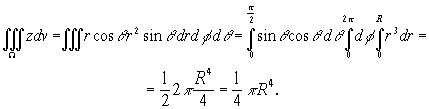
Так как объём полушара равен то

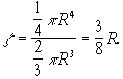
Перейдём к вычислению моментов инерции тела относительно координатных осей. Так как квадраты расстояний от точки P(x, y, z) до осей Ox, Oy, Oz соответственно равны то полагая для простоты получим следующие формулы :

Аналогично плоскому случаю интегралы

называются центробежными моментами инерции.

Для полярного момента инерции формула имеет вид

Если тело неоднородное, то в каждой формуле под знаком интеграла будет находиться дополнительный множитель - плотность тела в точке P.

Пример. Вычислим полярный момент инерции однородного шара радиуса R. В этом случае очень удобно перейти к сферическим координатам. Будем иметь

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки