Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

 

 

 

 

 

 

 

 

Рис.2

Если областью интегрирования служит внутренность параллелепипеда с гранями, параллельными координатным плоскостям (рис. 3), то пределы интегрирования постоянны во всех трех .интегралах :

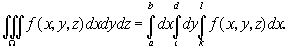
В этом случае интегрирование можно производить в любом порядке, пределы интегрирования будут при этом сохраняться.

Если же в общем случае менять порядок интегрирования ( т.е., скажем, интегрировать сначала по направлению оси Oy, а затем по области плоскости Oxz), то это приведёт к изменению порядка интегрирования в тройном интеграле и к изменению пределов интегрирования по каждой переменной.

 

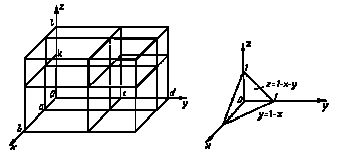
Рис.3 Рис.4

А) Пример.

Вычислим тройной интеграл

где - область, ограниченная координатными плоскостями

и плоскостью (пирамида, изображённая на рис.4).

Интегрирование по z совершается от z=0 до Поэтому, обозначая проекцию области на плоскость Oxy через D, получим

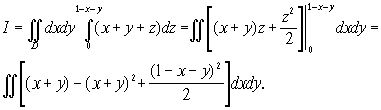
Расставим теперь пределы интегрирования по области D - треугольнику, уравнения сторон которого

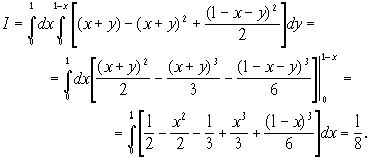
Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки