Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

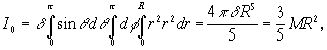
где М—масса шара.

Так как для сферы моменты инерции относительно осей координат, очевидно, равны между собой, то, учитывая, что получим

Моменты инерции тела относительно оси играют важную роль при вычислении кинетической энергии тела при его вращении около соответствующей оси. Пусть тело вращается около оси Оz с постоянной угловой скоростью . Найдем кинетическую энергию тела. Как известно, кинетическая энергия точки измеряется величиной , где т - масса точки, а - величина ее скорости. Кинетическая энергия системы точек определяется как сумма кинетических энергий отдельных точек, а кинетическая энергия тела - как сумма кинетических энергий всех частей, на которые оно разбито. Это обстоятельство позволяет применить для вычисления .кинетической энергии интеграл.

Возьмем какую-нибудь окрестность точки Р(х, у, z) тела . Величина линейной скорости точки Р при вращении около оси Оz равна и значит, кинетическая энергия части тела выразится так :

где - плотность тела в точке Р. Для кинетической энергии всего тела получаем

т.е.

Кинетическая энергия тела, вращающегося около некоторой оси с постоянной угловой скоростью, равна половине квадрата угловой скорости, умноженной на момент инерции тела относительно оси вращения.

 

 

 

 

 

 

 

 

 

 

 

 

 

Рекомендуем скачать другие рефераты по теме: налоги в россии, бесплатные тесты бесплатно.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки