Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

.

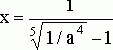            Принимая во внимание, что множество допустимых решений уравнения определяется условием , получаем окончательно:

            При  решением иррационального уравнения (20) будет

.

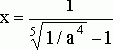            При всех остальных значениях  уравнение решений не имеет, т. е. множество его решений – пустое множество.

Уравнения, содержащие неизвестное под знаком абсолютной величины

Уравнения, содержащие неизвестное под знаком абсолютной величины, можно свести к уравнениям, не содержащим знака абсолютной величины, используя определение модуля. Так, например, решение уравнения

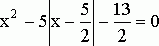                                                                                                              (21)

сводится к решению двух уравнений с дополнительными условиями.

            1) Если , то уравнение (21) приводится к виду

                                                            .                                                            (22)

            Решения этого уравнения: , . Условию  удовлетворяет второй корень квадратного уравнения (22), и число 3 является корнем уравнения (21).

            2) Если , уравнение (21) приводится к виду

.

            Корнями этого уравнения будут числа 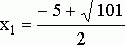 и 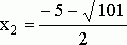. Первый корень  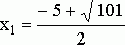не удовлетворяет условию  и поэтому не является решением данного уравнения (21).

            Таким образом, решениями уравнения (21) будут числа 3 и .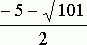

            Заметим, что коэффициенты уравнения, содержащего неизвестное под знаком абсолютной величины, можно подобрать таким образом, что решениями уравнения будут все значения неизвестного, принадлежащие некоторому промежутку числовой оси. Например, решим уравнение

                                                             .                                                             (23)

            Рассмотрим числовую ось Ох и отметим на ней точки 0 и 3 (ноли функций, стоящих под знаком абсолютной величины). Эти точки разобьют числовую ось на три промежутка  (рис. 1):

, , .

                                                            0                       3                              x

рис. 1.

            1) При   уравнение (23) приводится к виду

.

Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки