Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

                                                              ,                                                              (26)

где  - некоторое положительно число, отличное от единицы,  - любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению

.

В простейшем случае, когда , логарифмическое уравнение (26) имеет решение

.

Множество решений логарифмического уравнения вида , где  - некоторый многочлен указанного неизвестного, находится следующим образом.

Вводится новая переменная , и уравнение (25) решается как алгебраическое уравнение относительно . После этого решаются простейшие логарифмические уравнения вида (25).

П р и м е р 1. Решить уравнение

                                                    .                                                    (27)

            Относительно неизвестного  данное уравнение – квадратное:

.

            Корни этого уравнения: , .

            Решая логарифмические уравнения

, ,

получаем решения логарифмического уравнения (27): , .

            В некоторых случаях, для того чтобы свести решение логарифмического уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо предварительно сделать подходящие преобразования логарифмов, входящих в уравнение. Такими преобразованиями могут быть преобразование суммы логарифмов двух величин в логарифм произведения этих величин, переход от логарифма с одним основанием к логарифму с другим основанием и т. д.

            П р и м е р 2. Решить уравнение

                                            .                                            (28)

            Для того чтобы свести решение данного уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо прежде всего привести все логарифмы к одному основанию (здесь, например, к основанию 2). Для этого воспользуемся формулой

,

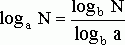в силу которой 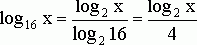. Подставив в уравнение (28) вместо  равную ему величину, получаем уравнение

.

            Заменой  это уравнение сводится к квадратному уравнению относительно неизвестного :

.

Корни этого квадратного уравнения: , . Решаем уравнения  и :

,

,

            П р и м е р 3. Решить уравнение

.

            Преобразуя разность логарифмов двух величин в логарифм частного этих величин:

,

сводим данное уравнение к простейшему логарифмическому уравнению

.

Заключение

            Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.

В данной работе были представлены далеко не все, способы решения уравнений и даже не все их виды, а только самые основные. Я надеюсь, что мое сочинение может послужить неплохим справочным материалом при решении тех или иных уравнений. В заключении хотелось бы отметить, что при написании данного сочинения я не ставил себе цели показать все виды уравнений, а излагал лишь имеющийся у меня материал.

Список использованной литературы

1. Глав. ред. М. Д. Аксенова. Энциклопедия для детей. Том 11. Математика. – М.: Аванта+, 1998. – 688 с.

2. Цыпкин А. Г. Под ред. С. А. Степанова. Справочник по математике для средней школы. – М.: Наука, 1980.- 400 с.

3. Г. Корн и Т. Корн. Справаочник по математике для начуных работников и инженеров. – М.: Наука, 1970.- 720 с.

[1]) Под допустимыми понимаются те численные значения букв, при которых выполнимы все операции, совершаемые над буквами, входящими в равенство. Например, допустимыми значениями букв, входящих в равенство

будут следующие; для ; для , для

[2]) Если a и b имеют разные знаки, то .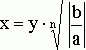

[3]) Случай ,  аналогичен разобранному.

[4]) Под алгебраическими преобразованиями уравнения

Понимают следующие преобразования:

1) прибавление к обеим частям уравнения одного и того же алгебраического выражения;

                2) умножение обеих частей уравнения на одно и то же алгебраическое выражение;

Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.



Предыдущая страница реферата | 12  13  14  15  16  17  18  19  20  21  22 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки