Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

.

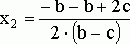
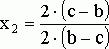
Двучленные уравнения

Уравнения n-й степени вида

                                                                                                                                (8)

называется двучленным уравнением. При  и  заменой [2])

,

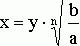где  - арифметическое значение корня, уравнение (8) приводится к уравнению

,

которое и будет далее рассматриваться.

Двучленное уравнение  при нечетном n имеет один действительный корень . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и  комплексных):

                   ( 0, 1, 2, ...,  ).                           (9)

            Двучленное уравнение  при четном n в множестве действительных чисел имеет два корня , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).

Двучленное уравнение  при четном n имеет один действительный корней , а в множестве комплексных чисел  корней, вычисляемых по формуле

    ( 0, 1, 2, ...,  ).                           (10)

Двучленное уравнение  при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет  корней, вычисляемых по формуле (10).

            Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.

            1) ().

            Уравнение имеет два действительных корня .

            2) ().

Уравнение имеет один дествительный корень  и два комплексных корня

.

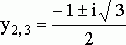            3)             ().

Уравнение имеет два действительных корния  и два комплексных корня .

            4)             ().

            Уравнение действительных корней не имеет. Комплексные корни: .

Рекомендуем скачать другие рефераты по теме: отчет о прохождении практики, ответы 7 класс.



Предыдущая страница реферата | 2  3  4  5  6  7  8  9  10  11  12 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки