Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

,

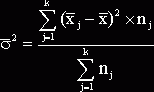где   k -  число групп;

 nj  - число единиц в j-ой группе;

 - частная средняя по j-ой группе;

  - общая средняя по совокупности единиц.

Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия σj2.

.

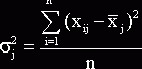Между общей дисперсией σ02, внутригрупповой дисперсией σ2 и межгрупповой дисперсией  существует соотношение:

σ02 =  + σ2.

Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе /2/.

1.2  Однофакторный дисперсионный анализ

Однофакторная дисперсионная модель имеет вид:

xij = μ + Fj + εij,             (1)

где  хij – значение исследуемой переменой, полученной на i-м уровне фактора (i=1,2,...,т) c j-м порядковым номером (j=1,2,...,n);

Fi – эффект, обусловленный влиянием i-го уровня фактора;

εij – случайная компонента, или возмущение, вызванное влиянием неконтролируемых факторов, т.е. вариацией переменой внутри отдельного уровня.

Основные предпосылки дисперсионного анализа:

-    математическое ожидание возмущения εij равно нулю для любых i,  т.е.

M(εij) = 0;             (2)

-     возмущения εij взаимно независимы;

- дисперсия переменной xij (или возмущения εij) постоянна для

любых i, j, т.е.

              D(εij) = σ2;                  (3)

- переменная xij (или возмущение εij) имеет нормальный закон

распределения N(0;σ2).

Влияние уровней фактора может быть как фиксированным или систематическим (модель I), так и случайным (модель II).

Рекомендуем скачать другие рефераты по теме: культурология как наука, сочинение тарас бульбо.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки