Комплексные числа ИСТОРИЧЕСКАЯ СПРАВКА

Комплексные числа были введены в математику для того, чтобы сделать возможной операцию извлечения квадратного корня из любого действительного числа. Это, однако, не является достаточным основанием для того, чтобы вводить в математику новые числа. Оказалось, что если производить вычисления по обычным правилам над выражениями, в которых встречаются квадратный корень из отрицательного числа, то можно прийти к результату, уже не содержащему квадратный корень из отрицательного числа. В XVI в. Кардано нашел формулу для решения кубического уравнения. Оказалось, когда кубическое уравнение имеет три действительных корня, в формуле Кардано встречается квадратный корень из отрицательного числа. Поэтому квадратные корни из отрицательных чисел стали употреблять в математике и назвали их мнимыми числами – тем самым они как бы приобрели право на нелегальное существование. Полные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, дал геометрическую интерпретацию и доказал основную теорему алгебры, утверждающую, что каждый многочлен имеет хотя бы один действительный корень.

1.ПОНЯТИЕ КОМПЛЕКСНОГО ЧИСЛА

Решение многих задач математики, физики сводится к решению алгебраических уравнений. Поэтому исследование алгебраических уравнений является одним из важнейших вопросов в математике. Стремление сделать уравнения разрешимыми – одна из главных причин расширения понятия числа.

Так для решимости уравнений вида X+A=B положительных чисел недостаточно. Например, уравнение X+5=2 не имеет положительных корней. Поэтому приходится вводить отрицательные числа и нуль.

На множестве рациональных чисел разрешимы алгебраические уравнения первой степени, т.е. уравнения вида A· X+B=0 (A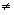0). Однако алгебраические уравнения степени выше первой могут не иметь рациональных корней. Например, такими являются уравнения X2=2, X3=5. Необходимость решения таких уравнений явилось одной из причин введения иррациональных чисел. Рациональные и иррациональные числа образуют множество действительных чисел.

Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Простейшее из них – уравнение X2+1=0. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.

Выясним предварительно, какой вид должны иметь комплексные числа. Будем считать, что на множестве комплексных чисел уравнение X2+1=0 имеет корень. Обозначим этот корень буквой i Таким образом, i – это комплексное число, такое, что i 2= –1.

Как и для действительных чисел, нужно ввести операции сложения и умножения комплексных чисел так, чтобы сумма и произведение их были бы комплексными числами. Тогда, в частности, для любых действительных чисел A и B выражение A+B· i можно считать записью комплексного числа в общем виде. Название “комплексное” происходит от слова “составное”: по виду выражения A+B· i.

Комплексными числами называют выражения вида A+B· i, где A и B –действительные числа, а i – некоторый символ, такой что i2= –1, и обозначают буквой Z.

Число A называется действительной частью комплексного числа A+B· i, а число B – его мнимой частью. Число i называется мнимой единицей.

Например, действительная часть комплексного числа 2+3· i равна 2, а мнимая равна 3.

Для строгого определения комплексного числа нужно ввести для этих чисел понятие равенства.

Два комплексных числа A+B· i и C+D· i называются равными тогда и только тогда, когда A=C и B=D, т.е. когда равны их действительные и мнимые части.

2.ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ КОМПЛЕКСНОГО ЧИСЛА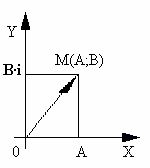

Действительные числа геометрически изображаются точками числовой прямой. Комплексное число A+B· i можно рассматривать как пару действительных чисел(A;B). Поэтому естественно комплексное число изображать точками плоскости. В прямоугольной системе координат комплексное число Z=A+B· i изображается точкой плоскости с координатами (A;B), и эта точка обозначается той же буквой Z (рисунок 1). Очевидно, что получаемое при этом соответствие является взаимно однозначным. Оно дает возможность интерпретировать комплексные числа как точки плоскости на которой выбрана система координат. Такая координатная плоскость называется комплексной плоскостью. Ось абсцисс называется действительной осью, т.к. на ней расположены точки соответствующие действительным числам. Ось ординат называется мнимой осью – на ней лежат точки, соответствующие мнимым комплексным числам.

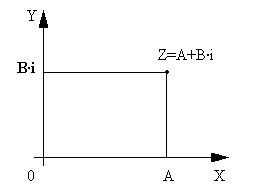
Не менее важной и удобной является интерпретация комплексного числа A+B· i как вектора, т.е. вектора с началом в точке

O(0;0) и с концом в точке М(A;B) (рисунок 2).

Соответствие установленное между множеством комплексных чисел, с одной стороны, и множествами точек или векторов плоскости, с другой, позволяет комплексные числа точками или векторами.

3.МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА

Пусть дано комплексное число Z=A+B· i. Сопряженным с Z называется комплексное число A – B· i, которое обозначается 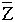, т.е.

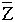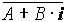==A – B· i.

Отметим, что 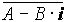= A+B· i, поэтому для любого комплексного числа Z имеет место равенство 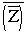=Z.

Модулем комплексного числа Z=A+B· i называется число 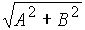и обозначается 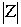, т.е.

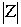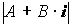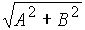== (1)

Из формулы (1) следует, что 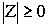для любого комплексного числа Z, причем 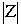=0 тогда и только тогда, когда Z=0, т.е. когда A=0 и B=0. Докажем, что для любого комплексного числа Z справедливы формулы:

4.СЛОЖЕНИЕ И УМНОЖЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ Суммой двух комплексных чисел A+B· i и C+D· i называется комплексное число (A+C) + (B+D)· i, т.е.(A+B· i) + (C+D· i)=(A+C) + (B+D)· i

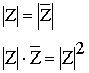
Произведением двух комплексных чисел A+B· i и C+D· i называется комплексное число (A· C – B· D)+(A· D+B· C) · i, т.е.

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.



1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки