
Комплексные числа
Категория реферата: Рефераты по математике
Теги реферата: реферат на тему организация, доклад
Добавил(а) на сайт: Остромир.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
Разделив обе части на Z2 получим:
Z=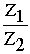
Из этого уравнения видно, что Z2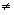 0
0
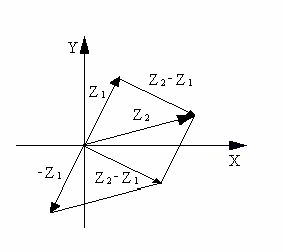
Геометрическое изображение разности комплексных чисел
Разности Z2– Z1 комплексных чисел Z1 и Z2, соответствует разность векторов, соответствующих числам Z1 и Z2. Модуль 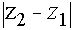 разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
разности двух комплексных чисел Z2 и Z1 по определению модуля есть длина вектора Z2– Z1. Построим этот вектор, как сумму векторов Z2 и (–Z1) (рисунок 4). Таким образом, модуль разности двух комплексных чисел есть расстояние между точками комплексной плоскости, которые соответствуют этим числам.
Это важное геометрическое истолкование модуля разности двух комплексных чисел позволяет с успехом использовать простые геометрические факты.
Пример 2: Даны комплексные числа Z1= 4 + 5·
i и Z2= 3 + 4·
i. Найти разность Z2 – Z1 и частное 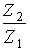
Z2 – Z1 = (3 + 4· i) – (4 + 5· i) = –1 – i
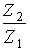 =
=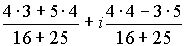 =
=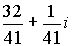
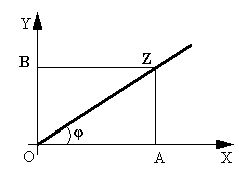
Запись комплексного числа Z в виде A+B· i называется алгебраической формой комплексного числа. Помимо алгебраической формы используются и другие формы записи комплексных чисел.
Рассмотрим тригонометрическую форму записи комплексного числа. Действительная и мнимая части комплексного числа Z=A+B·
i выражаются через его модуль 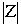 = r и аргумент j
следующим образом:
= r и аргумент j
следующим образом:
A= r· cosj ; B= r· sinj .
Число Z можно записать так:
Z= r·
cosj
+ i·
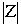 ·
sinj
= r·
(cosj
+ i·
sinj
)
·
sinj
= r·
(cosj
+ i·
sinj
)
Z = r· (cosj + i· sinj ) (2)
Эта запись называется тригонометрической формой комплексного числа.
r =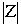 – модуль комплексного числа.
– модуль комплексного числа.
Число j называют аргументом комплексного числа.
Аргументом комплексного числа Z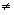 0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
0 называется величина угла между положительным направлением действительной оси и вектором Z, причем величина угла считается положительной, если отсчет ведется против часовой стрелки, и отрицательной, если производится по часовой стрелке.
Для числа Z=0 аргумент не определяется, и только в этом случае число задается только своим модулем.
Как уже говорилось выше 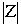 = r =
= r =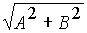 , равенство (2) можно записать в виде
, равенство (2) можно записать в виде
A+B·
i=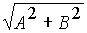 ·
cosj
+ i·
·
cosj
+ i·
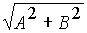 ·
sinj
, откуда приравнивая действительные и мнимые части, получим:
·
sinj
, откуда приравнивая действительные и мнимые части, получим:
cosj
=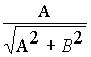 , sinj
=
, sinj
=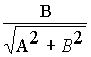 (3)
(3)
Если sinj поделить на cosj получим:
tgj
=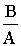 (4)
(4)
Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата