Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

(A + B· i)· (C + D· i)=(A· C – B· D) + (A· D + B· C)· i

Из формул вытекает, что сложение и умножение можно выполнять по правилам действий с многочленами, считая i2= –1. Операции сложения и умножения комплексных чисел обладают свойствами действительных чисел. Основные свойства:

Переместительное свойство:

Z1 +Z2=Z2+Z1, Z1· Z2=Z2· Z1

Сочетательное свойство:

(Z1+Z2)+Z3=Z1+(Z2+Z3), (Z1· Z2)· Z3=Z1· (Z2· Z3)

Распределительное свойство:

Z1· (Z2+Z3)=Z1· Z2+Z1· Z3

Геометрическое изображение суммы комплексных чисел

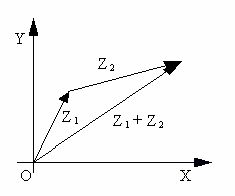
Согласно определению сложения двух комплексных чисел, действительная часть суммы равна сумме действительных частей слагаемых, мнимая часть суммы равна сумме мнимых частей слагаемых. Точно также определяются координаты суммы векторов:

Сумма двух векторов с координатами (A1;B1) и (A2;B2) есть вектор с координатами (A1+A2;B1+B2). Поэтому, чтобы найти вектор, соответствующий сумме комплексных чисел Z1 и Z2 нужно сложить векторы, соответствующие комплексным числам Z1 и Z2.

Пример 1: Найти сумму и произведение комплексных чисел Z1=2 – 3Ч i и

1 Способ:

Z2= –7 + 8Ч i.

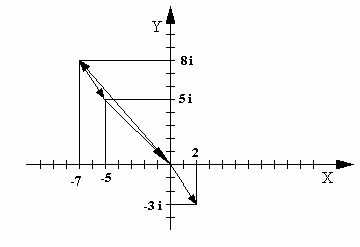
Z1 + Z2 = 2 – 7 + (–3 + 8)Ч i = –5 + 5Ч i

Z1Ч Z2 = (2 – 3Ч i)Ч (–7 + 8Ч i) = –14 + 16Ч i + 21Ч i + 24 = 10 + 37Ч i

2 Способ:

5.ВЫЧИТАНИЕ И ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ

Вычитание комплексных чисел – это операция, обратная сложению: для любых комплексных чисел Z1 и Z2 существует, и притом только одно, число Z, такое, что:

Z + Z2=Z1

Если к обеим частям равенства прибавить (–Z2) противоположное числу Z2:

Z+Z2+(–Z2)=Z1+(–Z2), откуда

Z = Z1 – Z2

Число Z=Z1+Z2 называют разностью чисел Z1 и Z2.

Деление вводится как операция, обратная умножению:

ZЧ Z2=Z1

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки