
Комплексные числа
Категория реферата: Рефераты по математике
Теги реферата: реферат на тему организация, доклад
Добавил(а) на сайт: Остромир.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
r = 1
Z = cos 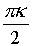 + iЧ
sin
+ iЧ
sin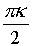
k = 0,1,2,3...
k = 0
Z1 = cos0+ iЧ sin0 = 1 + 0 = 1
k = 1
Z2 = cos 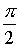 + iЧ
sin
+ iЧ
sin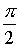 = 0 + i = i
= 0 + i = i
k = 2
Z3 = cosp + i·sinp = –1 + 0 = –1
k = 3
Z4 = cos 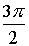 + iЧ
sin
+ iЧ
sin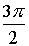
Ответ: Z13 = 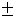 1
1
Z24 = 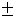 i
i
Из формулы 6 видно, что возведение комплексного числа r· ( cosj + i· sinj ) в целую положительную степень с натуральным показателем его модуль возводится в степень с тем же показателем, а аргумент умножается на показатель степени.
[ r· (cosj + i· sinj )]n= rn· ( cos nj + i· sin nj )
Число Z называется корнем степени n из числа w
( обозначается 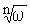 ), если Zn =w
.
), если Zn =w
.
Из данного определения вытекает, что каждое решение уравнения Zn = w
является корнем степени n из числа w
. Другими словами, для того, чтобы извлечь корень степени n из числа w
, достаточно решить уравнение Zn = w
. Если w
=0, то при любом n уравнение Zn = w
имеет только одно решение Z= 0. Если w
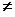 0, то и Z
0, то и Z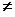 0, а, следовательно, и Z и w
можно представить в тригонометрической форме
0, а, следовательно, и Z и w
можно представить в тригонометрической форме
Z = r· (cosj + i· sinj ), w = p· (cosy + i· siny )
Уравнение Zn = w примет вид:
rn· ( cos nj + i· sin nj ) = p· ( cosy + i· siny )
Два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются слагаемыми, кратными 2p
. Следовательно, rn = p и nj
= y
+ 2p
k, где kО
Z
или r = 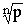 и j
=
и j
= 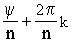 , где kО
Z
.
, где kО
Z
.
Итак, все решения могут быть записаны следующим образом:
ZK=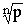 [cos(
[cos(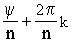 ) + i·
sin(
) + i·
sin(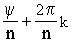 )], kО
Z
(8)
)], kО
Z
(8)
Формулу 8 называют второй формулой Муавра.
Таким образом, если w
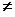 0, то существует ровно n корней степени n из числа w
: все они содержатся в формуле 8. Все корни степени n из числа w
имеют один и тот же модуль
0, то существует ровно n корней степени n из числа w
: все они содержатся в формуле 8. Все корни степени n из числа w
имеют один и тот же модуль 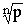 , но разные аргументы, отличающиеся слагаемым, кратным числу
, но разные аргументы, отличающиеся слагаемым, кратным числу 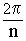 . Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w
, соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса
. Отсюда следует, что комплексные числа, являющиеся корнями степени n из комплексного числа w
, соответствует точкам комплексной плоскости, расположенным в вершинах правильного n – угольника, вписанного в окружность радиуса 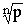 с центром в точке Z = 0.
с центром в точке Z = 0.
Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата