Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Эту формулу удобней использовать для нахождения аргумента j , чем формулы (3). Однако не все значения j , удовлетворяющие равенству (4), являются аргументами числа A+B· i . Поэтому при нахождении аргумента нужно учесть, в какой четверти расположена точка A+B· i.

7.СВОЙСТВА МОДУЛЯ И АРГУМЕНТА КОМПЛЕКСНОГО ЧИСЛА

С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.

Пусть Z1= r1· (cosj 1 + i· sinj 1), Z2 = r2· (cosj 2 + i· sinj 2). Тогда:

Z1Z2= r1· r2[cosj 1· cosj 2 – sinj 1· sinj 2 + i· ( sinj 1· cosj 2 + cosj 1· sinj 2)]=

= r1· r2[cos(j 1 + j 2) + i· sin(j 1 + j 2)].

Таким образом, произведение комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

Z1Z2= r1· r2[cos(j 1 + j 2) + i· sin(j 1 + j 2)] (5)

Из формулы (5) следует, что при умножении комплексных чисел их модули перемножаются, а аргументы складываются.

Если Z1=Z2 то получим:

Z2=[r· (cosj + i· sinj )]2= r2· (cos2j + i· sin2j )

Z3=Z2· Z= r2· (cos2j + i· sin2j )· r· (cosj + i· sinj )=

= r3· (cos3j + i· sin3j )

Вообще для любого комплексного числа Z= r· ( cosj + i· sinj )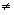0 и любого натурального числа n справедлива формула:

Zn =[ r· (cosj + i· sinj )]n= rn· ( cosnj + i· sinnj ), (6)

которую называют формулой Муавра.

Частное двух комплексных чисел, записанных в тригонометрической форме, можно находить по формуле:

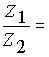
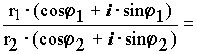
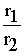[ cos(j 1 – j 2) + i· sin(j 1 – j 2)]. (7)

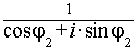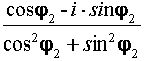= = cos(–j 2) + i· sin(–j 2)

Используя формулу 5

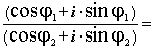(cosj 1 + i· sinj 1)Ч ( cos(–j 2) + i· sin(–j 2)) =

cos(j 1 – j 2) + i· sin(j 1 – j 2).

Пример 3:

Z3 = –8

Число –8 запишем в тригонометрической форме

8 = 8· ( cos(p + 2p k ) + i·sin(p + 2p k )), k О Z

Рекомендуем скачать другие рефераты по теме: образ сочинение, реферат бесплатно без регистрации.



Предыдущая страница реферата | 1  2  3  4  5  6  7  8  9  10  11 | Следующая страница реферата

Поделитесь этой записью или добавьте в закладки