Рефераты | Рефераты по математике | Математическая статистика Математическая статистика Категория реферата: Рефераты по математике Теги реферата: контрольная 2, древний реферат Добавил(а) на сайт: Кожевин. Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 | Следующая страница реферата 4	3	3	2	4	7	12	5
f i	0.100	0.075	0.075	0.050	0.100	0.175	0.300	0.125	1

Если мы усредним значения наблюдений, то формула расчета выборочного среднего

Mx = S Xi · ni =S Xi · fi {5–1} будет отличаться от выражения для математического ожидания m только использованием частот вместо вероятностей.

В нашем примере выборочное среднее значение составит Mx = 171.5 , но из этого пока еще нельзя сделать заключение о равенстве m = 171.5.

· Во-первых, Mx – это непрерывная СВ, следовательно, вероятность ее точного равенства чему-нибудь вообще равна нулю.

· Во-вторых, нас настораживает отсутствие ряда значений X.

· В-третьих, частоты наблюдений стремятся к вероятностям при бесконечно большом числе наблюдений, а у нас их только 40. Не мало ли?

Если мы усредним теперь значения квадратов отклонений наблюдений от выборочного среднего, то формула расчета выборочной дисперсии

Dx = (Sx)2 = S (Xi – Mx)2 · ni =S (Xi)2 · fi – (Mx)2 {5–2} также не будет отличаться от формулы, определяющей дисперсию s 2 .

В нашем примере выборочное значение среднеквадратичного отклонения составит Sx= 45.5 , но это совсем не означает, что s =45.5.

И всё же – как оценить оба параметра распределения или хотя бы один из них по данным наблюдений, т.е. по уже найденным Mx и Sx?

Прикладная статистика дает следующие рекомендации:

· значение дисперсии s 2 считается неизвестным и решается первый вопрос – достаточно ли число наблюдений N для того, чтобы использовать вместо величины s ее выборочное значение Sx;

· если это так, то решается второй вопрос – как построить нулевую гипотезу о величине математического ожидания m и как ее проверить.

Предположим вначале, что значение s каким–то способом найдено. Тогда формулируется простая нулевая гипотеза Њ0: m =Mx и осуществляется её проверка с помощью следующего критерия. Вычисляется вспомогательная функция (Z–критерий)

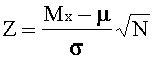, {5-3} значение и знак которой зависят от выбранного нами предполагаемого m .

Доказано, что значение Z является СВ с математическим ожиданием 0 , дисперсией 1 и имеет нормальное распределение.

Теперь важно правильно построить альтернативную гипотезу Њ1. Здесь чаще всего применяется два подхода.

Выбор одного из них зависит от того – большое или малое (по модулю) значение Z у нас получилось. Иными словами – как далеко от расчетного Mx мы выбрали гипотетическое m ..

· При малых отличиях между Mx и m разумно строить гипотезы в виде

Њ0: m = Mx;

Њ1: неизвестное нам значение m лежит в пределах

Mx – · Z 2k £ m £ Mx + · Z 2k {5–4}

Критическое (соответствующее уровню значимости в 5%) значение критерия составляет при этом = 1.96 (двухсторонний критерий). Если оказывается, что выборочное значение критерия ½ Z½ < 1.96, то гипотеза Њ0: m =Mx принимается, данные наблюдений не противоречат ей.

Если же это не так, то мы “в утешение” получаем информацию другого вида – где, на каком интервале находится искомое значение m .

· При больших отличиях (в большую или меньшую сторону) между m и Mx гипотезы строятся иначе Њ0: m = Mx; Њ1: неизвестное нам значение m лежит вне пределов, указанных в {5–4}.

Теперь критическое (соответствующее уровню значимости в 5%) значение критерия составляет Z 1k = 1.645 (односторонний критерий). Если оказывается, что выборочное значение критерия½ Z½ ³ 1.645, то гипотеза Њ0: m =Mx отвергается, данные наблюдений противоречат ей.

Если же это не так, то мы получаем информацию другого вида – где, на каком крае интервале находится искомое значение m . Разумеется, для других (не 5%) значений уровня значимости Z1k и Z 2k являются другими.

Чуть сложнее путь проверки гипотез о математическом ожидании m в случаях, когда s нам неизвестна и приходится довольствоваться выборочным значением среднеквадратичного отклонения по данным наблюдений.

В этом случае вместо “z –критерия” используется т.н. “t–критерий” или критерий Стьюдента

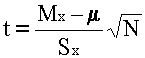, {5–5} в котором используется значение “несмещенной” оценки для дисперсии s 2

(Sx)2 = 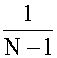S (Xi – Mx)2 · ni . {5–6}

Далее используется доказанное в теории положение – случайная величина t имеет специальное распределение Стьюдента с m=N–1 степенями свободы.

Существуют таблицы для этого распределения по которым можно найти вероятность ошибки первого рода или, что более удобно, – граничное значение этой величины при заданных заранее a и m. Таким образом, если вычисленное нами значение ½ t½ ³ t(a ,m), то Њ0 отвергается, если же это не так – Њ0 принимается. Конечно, при большом количестве наблюдений (N>100…120) различие между z– и t–критериями несущественно. Значения критерия Стьюдента для a =0.05 при разных количествах наблюдений составляют:

Таблица 5–3

Главная | Партнеры | Лучшие рефераты

Обратная связь

Рефераты | Рефераты по математике | Математическая статистика | страница реферата 22 | Большая Энциклопедия Рефератов от А до Я    Все рефераты, курсовые, дипломы, шпаргалки, сочинения, изложения, решебники, конспекты являются общедоступными    Копирование и размещение в интернете разрешается только при наличии активной индексируемой ссылки на Ahaha.ru

© 2006-2020 «Ahaha.ru»