Рефераты | Рефераты по математике | Математическая статистика Математическая статистика Категория реферата: Рефераты по математике Теги реферата: контрольная 2, древний реферат Добавил(а) на сайт: Кожевин. Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23 9	10	20	30	40	120
t	12.7	4.30	3.18	2.78	2.57	2.45	2.36	2.31	2.26	2.23	2.09	2.04	2.02	1.98

Оценка параметров дискретных распределений

В ряде случаев работы с некоторой дискретной СВ нам удается построить вероятностную схему событий, приводящих к изменению значений данной величины. Иными словами – закон распределения нам известен, но неизвестны его параметры. И наша задача – научиться оценивать эти параметры по данным наблюдений.

Начнем с наиболее простого случая. Пусть у нас есть основания считать, что случайная величина X может принимать целочисленные значения на интервале [0…k…n] с вероятностями

P(X=k)=pk(1– p)n-k,

т.е. распределена по биномиальному закону. Так вот, – единственный параметр p этого распределения нас как раз и интересует.

Примером подобной задачи является чисто практический вопрос о контроле качества товара.

Пусть мы решили оценить качество одной игральной кости из партии, закупленной для казино. Проведя n=200 бросаний мы обнаружили появлений цифры 6 в X = 25 случаях.

Выдвинем нулевую гипотезу Њ0: кость симметрична, то есть p= 1/6.

Вроде бы по наблюдениям частота выпадения цифры 6, составившая 25/200 не совпадает с гипотетическим значением вероятности 1/6. Но это чисто умозрительное, дилетантское заключение.

Теория прикладной статистики рекомендует вычислить значение непрерывной СВ

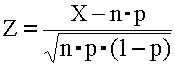, {5–7} т.е. использовать z–критерий (см. {5–3}).

В нашем примере наблюдаемое значение Z составит около –1.58. Следовательно, при пороговой вероятности в 5% условие ½ Z½ < 1.96 выполняется и у нас нет оснований отбрасывать нулевую гипотезу о симметрии игральной кости.

Отметим, что z–критерий позволяет решать еще одну важную задачу – о достаточном числе испытаний.

Пусть нам требуется проверить качество товара – некоторых изделий, каждое из которых может быть годным или негодным (бракованным). Пусть допустимый процент брака составляет p=5%. Ясно, что чем больше испытаний мы проведем, тем надежнее будет наш статистический вывод – браковать партию товара (например, – 10000 штук) или считать её пригодной.

Если мы провели n=500 проверок и обнаружили X=30 бракованных изделий, то выдвинув гипотезу Њ0: p=5% , мы найдем выборочное значение критерия по {5–7}. Оно составит около 1.03, что меньше “контрольного” 1.96 . Значит, у нас нет оснований браковать всю партию.

Но возникает вопрос – сколько проверок достаточно для принятия решения с уровнем значимости в 5%? Для этого достаточно учесть допустимый процент брака (т.е. задать p), указать допустимое расхождение между ним и наблюдаемым процентом брака в выборке (d= p–X/n) и воспользоваться выражением

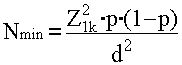{5–8}

Если мы примем d=± 0.02, то получим ответ – вполне достаточно 456 проверок, чтобы убедиться в том, что реальный процент брака отличается от допустимого не более чем на 2%.

Выборочные распределения на шкале Nom

Напомним, что случайная величина X, принимающая одно из n допустимых значений A, B, C и т.д. имеет номинальную шкалу тогда, когда для любой пары этих значений применимы только понятия “равно” или “неравно”.

Для подобных СВ не существует понятий математического ожидания, как и других моментов распределения. Но понятие закона распределения имеет смысл – это ряд вероятностей PA = P(X=A) для каждого из допустимых значений. Соответственно, итоги наблюдения над такой СВ дадут нам частоты fA. Если у нас имеется всего N наблюдений за такой величиной, то иногда имеется возможность выдвинуть и проверить гипотезы о природе такой случайной величины, ее законе распределения и параметрах этого закона. Ситуации, когда это возможно сделать, не так уж и редки – всё зависит от понимания нами природы, сути случайных событий, от многозначности случайной величины и, конечно же, от количества наблюдений.

Случай двухзначной случайной величины, N<50

Пусть нам крайне важно оценить "симметричность" некоторой случайной величины на номинальной двухпозиционной шкале со значениями "+" и "–" по наблюдениям за этой величиной. Если таких наблюдений было N+ =15 и N– = 25 соответственно, то это вся информация, которая у нас есть. Что же можно узнать из нее? Оказывается – достаточно много и иногда … даже надёжно!

В конце концов, мы можем полагать вероятность значения "+" на данной номинальной шкале равной p и тогда q = (1 – p) даст нам вероятность положения "–" на этой же шкале. Таким образом, мы уже построили закон распределения и дело остается за оценкой его единственного параметра p.

По сути дела у нас есть одна дискретная случайная величина – число появлений X на "первой" позиции своей номинальной шкалы и это число составляет S = N+ .

Но совершенно ясно, что новая случайная величина S имеет биномиальный закон распределения и вероятность наблюдения N+ =15 вполне можно вычислить, если знать или задаться значением p.
Скачали данный реферат: Каллисфен, Щеголев, Silaev, Косма, Pamfil, Chukchov.
Последние просмотренные рефераты на тему: оформление доклада, дипломы скачать бесплатно, контрольные 9 класс, объект реферата.

Предыдущая страница реферата | 13  14  15  16  17  18  19  20  21  22  23

Поделитесь этой записью или добавьте в закладки