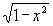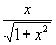Образцы исследования элементарных функций, содержащих обратные тригонометрические функции
Категория реферата: Рефераты по математике
Теги реферата: курсовая работа на тему бесплатно, исторические рефераты
Добавил(а) на сайт: Анисимов.
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата
|
X |
0 |
< x < |
1 |
< x < |
+∞ |
|
u=1/(x2-1) |
-1 |
↘ |
+ ∞ - ∞ |
↘ |
0 |
|
y=arctg(u) |
- π/4 |
↘ |
π/2 - π/2 |
↘ |
0 |
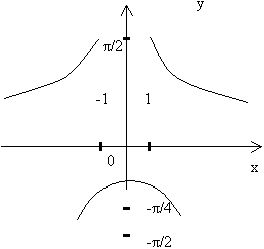Тригонометрические операции над аркфункциями
Тригонометрические функции от одного и того же аргумента выражаются алгебраически одна через другую, поэтому в результате выполнения какой-либо тригонометрической операции над любой из аркфункций получается алгебраическое выражение.
В силу определения аркфункций:
sin(arcsin(x)) = x , cos(arccos(x)) = x
(справедливо только для x є [-1;1] )
tg(arctg(x)) = x ,ctg(arcctg(x)) = x
(справедливо при любых x )
Графическое различие между функциями, заданными формулами:
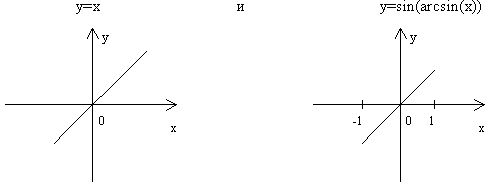
Сводка формул, получающихся в результате выполнения простейших тригонометрических операций над аркфункциями.
|
Аргумент функция |
arcsin(x) |
arccos(x) |
arctg(x) |
arcctg(x) |
||||
|
sin |
sin(arcsin(x))=x |
|
|
Предыдущая страница реферата | 1 2 3 4 5 6 7 8 9 10 11 | Следующая страница реферата Поделитесь этой записью или добавьте в закладкиКатегории: |
